
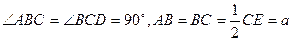 ,D是CE的中点,点M和点N在
,D是CE的中点,点M和点N在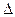 ADE绕AD向上翻折的过程中,分别以
ADE绕AD向上翻折的过程中,分别以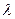 的速度,同时从点A和点B沿AE和BD各自匀速行进,t 为行进时间,0
的速度,同时从点A和点B沿AE和BD各自匀速行进,t 为行进时间,0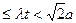 。
。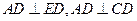 ,所以AD⊥平面CDE,ED是AE在平面CDE上的射影,∠AED=450,所以直线AE与平面CDE所成的角为450………………………………4分
,所以AD⊥平面CDE,ED是AE在平面CDE上的射影,∠AED=450,所以直线AE与平面CDE所成的角为450………………………………4分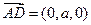 ………5分
………5分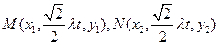 ,
, 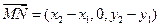 …………9分
…………9分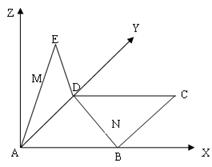
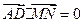 ,得
,得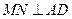 ,而
,而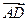 是平面CDE的一个法向量,且
是平面CDE的一个法向量,且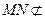 平面CDE,
平面CDE,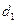 ,点N到平面CDE的距离为
,点N到平面CDE的距离为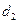 ,则
,则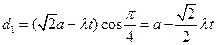 ,同理
,同理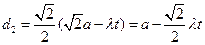
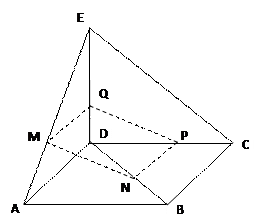 所以
所以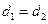 ,故MN//平面CDE……………………………………………………………14分
,故MN//平面CDE……………………………………………………………14分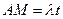 ,
, ………………7分
………………7分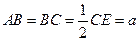 ,点D是CE的中点,得
,点D是CE的中点,得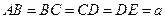 ,四边形ABCD为正方形,⊿ADE为等腰三角形.
,四边形ABCD为正方形,⊿ADE为等腰三角形. 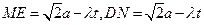 ……………………10分
……………………10分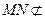 平面CDE,
平面CDE,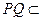 平面CDE,所以MN//平面CDE……………………………………………………14分
平面CDE,所以MN//平面CDE……………………………………………………14分

科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
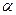 内作菱形ABCD,边长为1,∠BAD=60°,再在
内作菱形ABCD,边长为1,∠BAD=60°,再在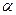 的上方,分别以△
的上方,分别以△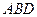 与△
与△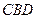 为底面安装上相同的正棱锥P-ABD与Q-CBD,∠APB=90°.
为底面安装上相同的正棱锥P-ABD与Q-CBD,∠APB=90°.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
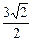
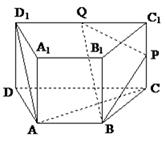
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
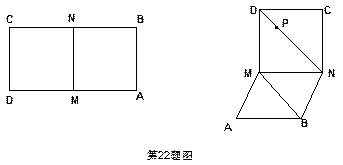
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
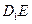 ⊥平面AB1F时,求二面角C1—EF—A的大小(结果用反三角函数值表示).
⊥平面AB1F时,求二面角C1—EF—A的大小(结果用反三角函数值表示).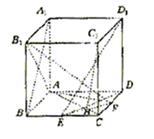
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com