
分析 (1)直接代入即可获得解答;
(2)根据函数单调性的定义,首先应在所给区间上任设两个数并规定大小,然后通过作差法分析获得两数对应函数值之间的大小关系即可;
(3)充分利用好函数的奇偶性,即可求的a的值,通过讨论x的范围,判断出|f(x)|、f(2)的大小关系.
解答 解:(1)a=1时:f(0)=1-$\frac{1}{{2}^{0}+1}$=$\frac{1}{2}$;
(2)∵f(x)的定义域为R∴任取x1x2∈R且x1<x2
则f(x1)-f(x2)=a-$\frac{1}{{2}^{{x}_{1}}+1}$-a+$\frac{1}{{2}^{{x}_{2}}+1}$=$\frac{{2}^{{x}_{1}}{-2}^{{x}_{2}}}{{(2}^{{x}_{1}}+1){(2}^{{x}_{2}}+1)}$.
∵y=2x在R是单调递增且x1<x2
∴0<2x1<2x2,∴2x1-2x2<0,
2x1+1>0,2x2+1>0,
∴f(x1)-f(x2)<0
即f(x1)<f(x2),
∴f(x)在R上单调递增.
(3)∵f(x)是奇函数∴f(-x)=-f(x),
即a-$\frac{1}{{2}^{-x}+1}$=-a+$\frac{1}{{2}^{x}+1}$,
解得:a=1.
∴f(ax)=f(x)
又∵f(x)在R上单调递增
∴x>2或x<-2时:|f(x)|>f(2),
x=±2时:|f(x)|=f(2),
-2<x<2时:|f(x)|<f(2).
点评 本题考查的是函数单调性、奇偶性等知识的综合问题.在解答的过程当中充分体现了计算的能力、单调性定义的应用以及问题转化的能力.值得同学们体会和反思.


科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{1}{4}$) | B. | (-$\frac{1}{4}$,+∞) | C. | (0,+∞) | D. | (-∞,-$\frac{1}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
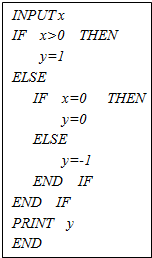 读程序,回答下列问题:
读程序,回答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com