
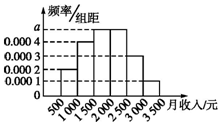
 统计局就某地居民的月收入情况调查了10 000人,并根据所得数据画了样本频率分布直方图,每个分组包含左端点,不包含右端点.
统计局就某地居民的月收入情况调查了10 000人,并根据所得数据画了样本频率分布直方图,每个分组包含左端点,不包含右端点.分析 (1)先求出[2000,2500)的频率,利用频率乘以样本容量求出在[2000,2500)的人数.
(2)根据频率直方图,利用频率是纵坐标乘以组距,先确定中位数的位置,再由公式计算出中位数;
(3)利用数据的平均数是图中各小长方形底边中点的坐标与对应频率的乘积和,由频率分布直方图,求出样本数据的平均数即可.
解答 (本题满分为12分)
解:(1)因为(0.0002+0.0004+0.0003+0.0001)×500=0.5,所以a═0.0005,月收入在2000元~2500元的频率为0.25,
所以抽取的100人中月收入在2000元~2500元的人数为0.25×100=25.
(2)因为0.0002×(1000-500)=0.1,0.0004×(1500-1000)=0.2,
0.0005×(2000-1500)=0.25,0.1+0.2+0.25=0.55>0.5,
所以样本数据的中位数是1500+$\frac{0.5-(0.+0.2)}{0.0005}$=1500+400=1900(元).
(3)(750×0.0002+1250×0.0004+1750×0.0005+2250×0.0005+2750×0.0003+3250×0.0001)×500=1900(元).
所以样本数据的平均数为1900元.
点评 本题考查频率分布直方图及分层抽样的方法,求解此类题的关键是熟练掌握频率分布直方图的结构及分层抽样的规则,本题属于统计中的基本题型,是这几年高考的热点,在高考的试卷上出现的频率相当高,应对此类题做题的规律好好理解掌握.频率分布直方图中小长方形的面积=组距×$\frac{频率}{组距}$=频率,各个矩形面积之和等于1,能根据直方图求频率,属于常规题型.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3,13,23,33,43 | B. | 7,12,23,36,41 | C. | 5,10,15,20,25 | D. | 9,16,25,36,49 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com