
分析 由题意求解集合A和集合B,根据A∪B=R,建立关系求实数a取值范围.
解答 解:由题意:函数f(x)=$\sqrt{{x}^{2}-16}$的定义域需满足:x2-16≥0,
解得:x≤-4或x≥4,
∴集合A={x|x≤-4或x≥4},
函数g(x)=x2-2x+a=(x-1)2+a-1
∵x∈[0,4]
当x=1时,函数g(x)取得最小值为a-1;
当x=4时,函数g(x)取得最大值为a+8;
∴函数g(x)值域为[a-1,a+8]
∴集合B=[a-1,a+8]
∵A∪B=R,
∴需满足:$\left\{\begin{array}{l}{a-1≤-4}\\{a+8≥4}\end{array}\right.$
解得:-4≤a≤-3
故得实数a的取值范围为[-4,-3].
点评 本题考查了函数的定义域和值域的求法和集合的基本运算.属于基础题.


 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源: 题型:选择题
| A. | 方程x2-2x+y2+4y+5=0表示一个点 | |
| B. | 若m>n>0,则方程mx2+ny2=1表示焦点在y轴上的椭圆 | |
| C. | 已知点M(-2,0)、N(2,0),若|PM|-|PN|=4,则动点P的轨迹是双曲线的一支 | |
| D. | 以过抛物线y2=2px(p≠0)焦点的弦为直径的圆与抛物线准线的位置关系是相切 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,3) | B. | (-3,1) | C. | (-1,-3 ) | D. | (3,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
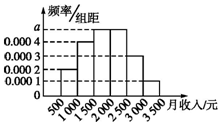 统计局就某地居民的月收入情况调查了10 000人,并根据所得数据画了样本频率分布直方图,每个分组包含左端点,不包含右端点.
统计局就某地居民的月收入情况调查了10 000人,并根据所得数据画了样本频率分布直方图,每个分组包含左端点,不包含右端点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com