C
分析:①根据诱导公式化简,即可得到y=cos
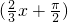
是奇函数,从而正确;
②求出sinα+cosα的最大值,发现最大值

<

,从而可得到不存在实数α,使得sinα+cosα=

;
③找两个特殊角α、β,满足α<β,比如45°<30°+360°,但是tan45°>tan(30°+360°)不满足要求,故不对;
④把x=

代入得到y=sin(2x+

)=sin

=-1,x=

是函数y=sin(2x+

)的一条对称轴;
⑤把x=

代入得到y=sin
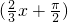
=sin

=1,故点
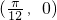
不是函数y=sin
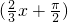
的对称中心.
解答:①函数y=cos
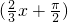
=-sin
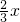
是奇函数;
②由sinα+cosα=

sin(

)的最大值为

,
因为

<

,所以不存在实数α,使得sinα+cosα=

;
③α,β是第一象限角且α<β.例如:45°<30°+360°,
但tan45°>tan(30°+360°),即tanα<tanβ不成立;
④把x=

代入y=sin(2x+

)=sin

=-1,
所以x=

是函数y=sin(2x+

)的一条对称轴;
⑤把x=

代入函数y=sin
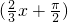
=sin

=1,
所以点
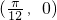
不是函数y=sin
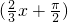
的对称中心.
综上所述,只有①④正确.
故选C.
点评:本题主要考查诱导公式的应用、正弦函数的基本性质--最值、对称性.三角函数的内容比较琐碎,要记忆的比较多,平时要注意公式的记忆和基础知识的积累.

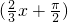 是奇函数;②存在实数α,使得sin α+cos α=
是奇函数;②存在实数α,使得sin α+cos α= ;③若α、β是第一象限角且α<β,则tan α<tan β;④x=
;③若α、β是第一象限角且α<β,则tan α<tan β;④x= 是函数y=sin
是函数y=sin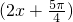 的一条对称轴方程;⑤函数y=sin
的一条对称轴方程;⑤函数y=sin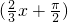 的图象关于点
的图象关于点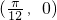 成中心对称图形.其中正确的序号为
成中心对称图形.其中正确的序号为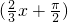 是奇函数,从而正确;
是奇函数,从而正确; <
< ,从而可得到不存在实数α,使得sinα+cosα=
,从而可得到不存在实数α,使得sinα+cosα= ;
; 代入得到y=sin(2x+
代入得到y=sin(2x+ )=sin
)=sin =-1,x=
=-1,x= 是函数y=sin(2x+
是函数y=sin(2x+ )的一条对称轴;
)的一条对称轴; 代入得到y=sin
代入得到y=sin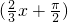 =sin
=sin =1,故点
=1,故点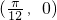 不是函数y=sin
不是函数y=sin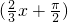 的对称中心.
的对称中心.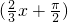 =-sin
=-sin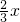 是奇函数;
是奇函数; sin(
sin( )的最大值为
)的最大值为 ,
, <
< ,所以不存在实数α,使得sinα+cosα=
,所以不存在实数α,使得sinα+cosα= ;
; 代入y=sin(2x+
代入y=sin(2x+ )=sin
)=sin =-1,
=-1, 是函数y=sin(2x+
是函数y=sin(2x+ )的一条对称轴;
)的一条对称轴; 代入函数y=sin
代入函数y=sin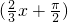 =sin
=sin =1,
=1,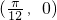 不是函数y=sin
不是函数y=sin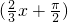 的对称中心.
的对称中心.

 口算能手系列答案
口算能手系列答案