
【题目】(10分)设![]() 和
和![]() 分别是先后抛掷一枚骰子得到的点数,用随机变量
分别是先后抛掷一枚骰子得到的点数,用随机变量![]() 表示方程
表示方程
![]() 实根的个数(重根按一个计).
实根的个数(重根按一个计).
(Ⅰ)求方程![]() 有实根的概率;
有实根的概率;
(Ⅱ)求![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)求在先后两次出现的点数中有5的条件下,方程![]() 有实根的概率.
有实根的概率.
【答案】(Ⅰ)![]()
(Ⅱ)
![]()
(Ⅲ)![]()
【解析】本试题主要考查了古典概型概率的计算,以及分布列和数学期望的求解的综合运用。
(1)中理解本题是一个等可能事件的概率,试验发生包含的基本事件总数为6×6=36,那么借助于使方程有实根△=b2-4c≥0,得到事件A发生的基本事件数,得到概率值。
(2)利用ξ=0,1,2的可能取值,分别得到各个取值的概率值,然后写出分布列和数学期望值
(3)分析在先后两次出现的点数中有5的条件下,方程x2+bx+c=0有实根,这是一个条件概率,利用条件概率公式得到结论。
解:(I)由题意知,本题是一个等可能事件的概率,
试验发生包含的基本事件总数为6×6=36,
满足条件的事件是使方程有实根,则△=b2-4c≥0,即.
下面针对于c的取值进行讨论
当c=1时,b=2,3,4,5,6; 当c=2时,b=3,4,5,6;
当c=3时,b=4,5,6; 当c=4时,b=4,5,6;
当c=5时,b=5,6; 当c=6时,b=5,6,
目标事件个数为5+4+3+3+2+2=19,
因此方程![]() 有实根的概率为
有实根的概率为![]()
(II)由题意知用随机变量ξ表示方程![]() 实根的个数得到
实根的个数得到
ξ=0,1,2 根据第一问做出的结果得到
则![]() ,
,![]() ,
,![]() ,
,
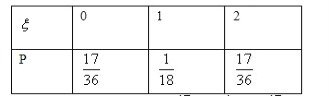
∴ξ的分布列为

∴ξ的数学期望 ![]()
(III)在先后两次出现的点数中有5的条件下,方程x2+bx+c=0有实根,
这是一个条件概率,
记“先后两次出现的点数中有5”为事件M,
“方程![]() 有实根”为事件N,
有实根”为事件N,
则,![]() ,
,![]() ∴
∴![]()


科目:高中数学 来源: 题型:
【题目】试求下列函数的定义域与值域:
(1)f(x)=(x-1)2+1,x∈{-1,0,1,2,3};
(2)f(x)=(x-1)2+1;
(3)f(x)=![]() ;
;
(4)f(x)=x-![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知幂函数f(x)=x![]() (m∈N*).
(m∈N*).
(1)试确定该函数的定义域,并指明该函数在其定义域上的单调性;
(2)若该函数还经过点(2, ![]() ),试确定m的值,并求满足条件f(2-a)>f(a-1)的实数a的取值范围.
),试确定m的值,并求满足条件f(2-a)>f(a-1)的实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2015男篮亚锦赛决赛阶段,中国男篮以9连胜的不败战绩赢得第28届亚锦赛冠军,同时拿到亚洲唯一1张直通里约奥运会的入场券,赛后,中国男篮主力易建联荣膺本届亚锦赛![]() (最有价值球员),下表是易建联在这9场比赛中投篮的统计数据.
(最有价值球员),下表是易建联在这9场比赛中投篮的统计数据.
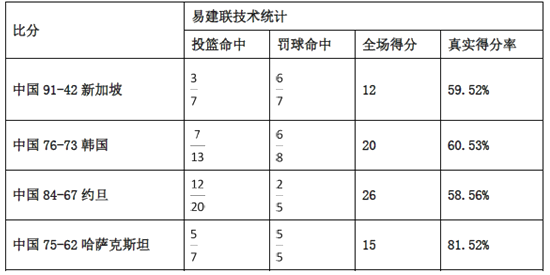
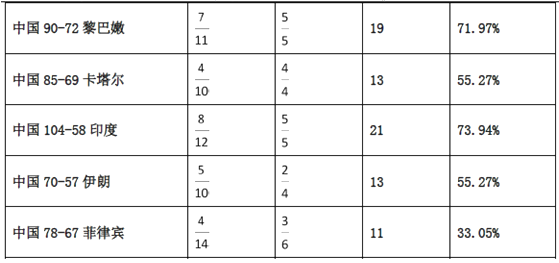
注:(1)表中![]() 表示出手
表示出手![]() 次命中
次命中![]() 次;
次;
(2)![]() (真实得分率)是衡量球员进攻的效率,其计算公式为:
(真实得分率)是衡量球员进攻的效率,其计算公式为:
![]()
![]()
(1)从上述9场比赛中随机选择一场,求易建联在该场比赛中![]() 超过50%的概率;
超过50%的概率;
(2)从上述9场比赛中随机选择一场,求易建联在该场比赛中![]() 至少有一场超过60%的概率;
至少有一场超过60%的概率;
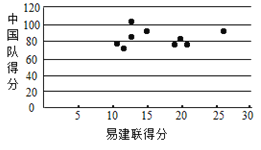
(3)用![]() 来表示易建联某场的得分,用
来表示易建联某场的得分,用![]() 来表示中国队该场的总分,画出散点图如图所示,请根据散点图判断
来表示中国队该场的总分,画出散点图如图所示,请根据散点图判断![]() 与
与![]() 之间是否具有线性相关关系?结合实际简单说明理由.
之间是否具有线性相关关系?结合实际简单说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义在区间
是定义在区间![]() 上的奇函数,且
上的奇函数,且![]() 若对于任意的
若对于任意的![]() 有
有![]()
(1)判断并证明函数的单调性;
(2)解不等式![]() ;
;
(3)若![]() 对于任意的
对于任意的![]() ,
, ![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
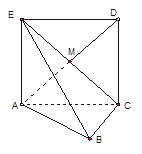
【题目】如图,边长为2的正方形ACDE所在的平面与平面ABC垂直,AD与CE的交点为M,![]() ,且AC=BC.
,且AC=BC.
(1)求证:![]() 平面EBC;
平面EBC;
(2)求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某理科考生参加自主招生面试,从7道题中(4道理科题3道文科题)不放回地依次任取3道作答.
(1)求该考生在第一次抽到理科题的条件下,第二次和第三次均抽到文科题的概率;
(2)规定理科考生需作答两道理科题和一道文科题,该考生答对理科题的概率均为![]() ,答对文科题的概率均为
,答对文科题的概率均为![]() ,若每题答对得10分,否则得零分.现该生已抽到三道题(两理一文),求其所得总分
,若每题答对得10分,否则得零分.现该生已抽到三道题(两理一文),求其所得总分![]() 的分布列与数学期望
的分布列与数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com