
| 2 |
| a |
| b |
| 1 |
| 2 |
| 2 |
| 11 | m |
| �� |
| 3 |
| 2 |
| �� |
| 4 |
| 2 |
| a |
| sinA |
| b |
| sinB |
| 3 |
| sin45�� |
2
| ||
| sinB |
| 2 |
| 3 |
| a |
| b |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| �� |
| 3 |
| 2 |
| �� |
| 4 |
| �� |
| 4 |
| �� |
| 4 |
| 7�� |
| 12 |
| ||
| 2 |
| �� |
| 4 |
| 2 |
| 11 | m |


 �������Ͽ��㱾ϵ�д�
�������Ͽ��㱾ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 2 |
| 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| x |
| x2+1 |
| 3 |
| 4 |
| 1 |
| 3 |
| 3 |
| 10 |
| 3 |
| 4 |
| a |
| a2+1 |
| b |
| b2+1 |
| c |
| c2+1 |
| 9 |
| 10 |
| n |
 |
| k=1 |
| ak | ||
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014��ɽ��ʡ�����и�����ѧ�ڵ�һ���¿�������ѧ�Ծ��������棩 ���ͣ������
������������������__________(�����)��
��f(x)��ax2��bx��c��[0������)������������һ����������ǣ� ��0��
��0��
����֪�ף�x��y��3���ң�x��1��y��2��������ҵij�ֲ���Ҫ������
������{an}(n��N*)�ǵȲ����еij�Ҫ������Pn �ǹ��ߵģ�
�ǹ��ߵģ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014�츣��ʡ�߶���ѧ�����п���������ѧ�Ծ��������棩 ���ͣ������
���������ĸ����ۣ��� 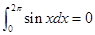 ��
��
����֪���� ����
���� ����
���� 1
1
����֪ Ϊ������R�ϵĿɵ�����,��
Ϊ������R�ϵĿɵ�����,�� ����
���� �����,����
�����,���� ,
,  ��
��
�� ������������������Լ����ϵĶ�Ԫ���� ���㣺��1��
���㣺��1�� ����2��
����2�� ��3��
��3�� ����
���� =
=
��������ȷ���۵��� ����д����Ϊ��ȷ����ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
������������������__________(�����)��
��f(x)��ax2��bx��c��[0������)������������һ����������ǣ�![]() ��0��
��0��
����֪�ף�x��y��3���ң�x��1��y��2��������ҵij�ֲ���Ҫ������
������{an}(n��N*)�ǵȲ����еij�Ҫ������Pn![]() �ǹ��ߵģ�
�ǹ��ߵģ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com