
分析 先求出关于p,q的x的范围,结合充分必要条件的定义判断即可.
解答 解:(1)∵P={x|x2-$\frac{3}{2}$x+$\frac{1}{2}$≤0}={x|$\frac{1}{2}$≤x≤1},
S={x|x2-(2a+1)x+a(a+1)≤0}={x|a≤x≤a+1},
若x∈P是x∈S的充要条件,则$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{a+1=1}\end{array}\right.$,无解,
故不存在a满足条件;
(2)若x∈P是x∈S的必要不充分条件,则$\left\{\begin{array}{l}{a≥\frac{1}{2}}\\{a+1≤1}\end{array}\right.$,无解,
故不存在a满足条件.
点评 本题考查了充分必要条件,考查解不等式问题,是一道基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[\frac{1}{6},\frac{1}{2})$ | B. | $[\frac{1}{3},\frac{1}{2}]$ | C. | $(\frac{1}{6},\frac{1}{2}]$ | D. | $[\frac{1}{3},\frac{1}{2}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
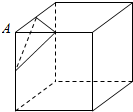 如图,设A是棱长为2的正方体的一个顶点,过从顶点A出发的三条棱的中点作截面,对正方体的所有顶点都如此操作,截去8个三棱锥,所得的各截面与正方体各面共同围成一个多面体,则关于此多面体有以下结论:
如图,设A是棱长为2的正方体的一个顶点,过从顶点A出发的三条棱的中点作截面,对正方体的所有顶点都如此操作,截去8个三棱锥,所得的各截面与正方体各面共同围成一个多面体,则关于此多面体有以下结论:| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com