
分析 (Ⅰ)设等差数列{an}的公差为d,等比数列{bn}的公比为q,由已知列式求得首项和等差数列的公差及等比数列的公比,则数列{an}、{bn}通项公式可求;
(Ⅱ)把数列{an}、{bn}通项公式代入cn=$\frac{{2{a_n}}}{b_n}$,然后利用错位相减法求得数列{cn}的前n项和为Cn.
解答 解:(Ⅰ)设等差数列{an}的公差为d,等比数列{bn}的公比为q,
则$\left\{\begin{array}{l}{a_1}={b_1}\\ 2({{a_1}+d})={b_1}q\\ 2{a_1}+d+{b_1}+{b_1}q=13\\ 2({3{a_1}+3d})={b_1}{q^2}\end{array}\right.$,解得$\left\{\begin{array}{l}{a_1}=2\\{b_1}=2\\ d=1\\ q=3\end{array}\right.$,
故${a_n}=n+1,{b_n}=2•{3^{n-1}}$;
(Ⅱ)由(Ⅰ)得:cn=$\frac{{2{a_n}}}{b_n}$=$\frac{n+1}{{3}^{n-1}}$,
∴${C}_{n}={c}_{1}+{c}_{2}+…+{c}_{n}=2+3×\frac{1}{3}+4×\frac{1}{{3}^{2}}+…+(n+1)×\frac{1}{{3}^{n-1}}$,
$3{C}_{n}=2×3+3×1+4×\frac{1}{3}+…+(n+1)×\frac{1}{{3}^{n-2}}$.
两式相减得:$2{C_n}=7+\frac{1}{3}+\frac{1}{3^2}+…+\frac{1}{{{3^{n-2}}}}-({n+1})×\frac{1}{{{3^{n-1}}}}=7+\frac{{\frac{1}{3}-{{({\frac{1}{3}})}^{n-1}}}}{{1-\frac{1}{3}}}-({n+1})×\frac{1}{{{3^{n-1}}}}$
=$7+\frac{1}{2}-\frac{1}{2}{({\frac{1}{3}})^{n-2}}-({n+1})×\frac{1}{{{3^{n-1}}}}=\frac{15}{2}-\frac{2n+5}{{2•{3^{n-1}}}}$.
∴${C_n}=\frac{15}{4}-\frac{2n+5}{{4•{3^{n-1}}}}$.
点评 本题考查等差数列与等比数列的通项公式,考查了错位相减法求数列的前n项和,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | 2016 | B. | -2016 | C. | 2017 | D. | -2017 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -12 | B. | -6 | C. | 12 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-1≤x<1} | B. | {-1,0,1} | C. | {-1,0} | D. | {0,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{11}{3}$,-3] | B. | [-6,-4] | C. | [-3,-2$\sqrt{2}}$] | D. | [-4,-3] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
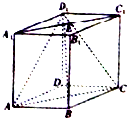 已知四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD,底面ABCD为菱形.
已知四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD,底面ABCD为菱形.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | 16 | C. | 18 | D. | 24 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
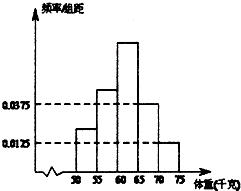 为了解某校高三毕业生报考体育专业学生的体重(单位:千克),将他们的体重数据整理后得到如下频率分布直方图,已知图中从左到右前3个小组的频率之比为1:2:3,其中第二小组的频数为8.
为了解某校高三毕业生报考体育专业学生的体重(单位:千克),将他们的体重数据整理后得到如下频率分布直方图,已知图中从左到右前3个小组的频率之比为1:2:3,其中第二小组的频数为8.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com