
分析 由题意画出图形,在直线a上取一点P,过P作PB⊥β,则PA、PB确定平面PAB,设平面PAB交直线l于点O,可得∠AOB为二面角的平面角等于60°,设a交β于C,可得B、O、C共线,P、B、C共面,得到∠PCB是PA与平面β所成的角,由三角形外角与不相邻内角的关系得答案.
解答 解:如图,直线a⊥α,垂足为A,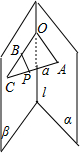
在直线a上取一点P,过P作PB⊥β,则PA、PB确定平面PAB,设平面PAB交直线l于点O,
∴l⊥平面PAO,则l⊥OA,l⊥OB,
∵二面角α-1-β的大小是60°,PA⊥α,PB⊥β,
∴∠AOB=60°,则∠APB=120°,
如图,设a交β于C,∴B、O、C共线,P、B、C共面,
∴∠PCB是PA与平面β所成的角,
∵∠APB=120°,∠PBC=90°,
∴∠PCB=30°.
即直线a与平面β所成角的大小为30°.
故答案为:30°.
点评 本题考查线面角的求法,考查空间想象能力和思维能力,是中档题.


 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:解答题
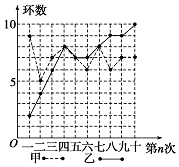 甲、乙两人在相同条件下各射靶10次,每次射靶的成绩情况如图所示:
甲、乙两人在相同条件下各射靶10次,每次射靶的成绩情况如图所示:| 平均数 | 方差 | 命中9环及9环以上的次数 | |
| 甲 | |||
| 乙 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
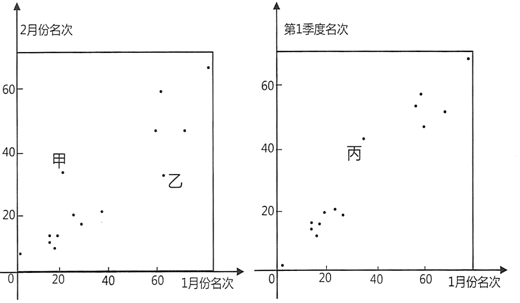
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | (1,4) | C. | (1,4] | D. | (0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com