
分析 作出不等式组对应的平面区域,根据直线和区域的关系即可得到结论.
解答 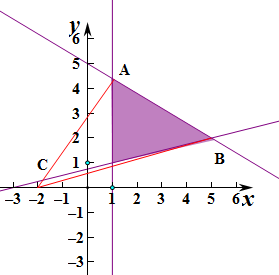 解:作出不等式组对应的平面区域,
解:作出不等式组对应的平面区域,
直线y=k(x+2)过定点(-2,0),
由图象可知当直线l经过点A时,直线斜率最大,当经过点B时,直线斜率最小,
由$\left\{\begin{array}{l}{x=1}\\{3x+5y=25}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=1}\\{y=\frac{22}{5}}\end{array}\right.$,即A(1,$\frac{22}{5}$),此时k=$\frac{\frac{22}{5}-0}{1-(-2)}$=$\frac{22}{15}$,
由$\left\{\begin{array}{l}{x-4y=-3}\\{3x+5y=25}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=5}\\{y=2}\end{array}\right.$,即B(5,2),此时k=$\frac{2-0}{5-(-2)}$=$\frac{2}{7}$,
故k的取值范围是$[\frac{2}{7},\frac{22}{15}]$,
故答案为:$[\frac{2}{7},\frac{22}{15}]$
点评 本题主要考查线性规划的应用以及直线斜率的公式的计算,利用数形结合是解决此类问题的基本方法.


 智能训练练测考系列答案
智能训练练测考系列答案科目:高中数学 来源: 题型:选择题
| A. | 某校高三8个班,1班51人,2班53人,3班52人,由此推测各班人数都超过50人 | |
| B. | 由三角形的性质,推测空间四面体的性质 | |
| C. | 平行四边形的对角线互相平分,菱形是平行四边形,所以菱形的对角线互相平分 | |
| D. | 在数列{an}中,${a_1}=1,{a_n}=\frac{1}{2}({{a_{n-1}}+\frac{1}{{{a_{n-1}}}}})({n≥2})$,通过计算a2,a3,a4推理出{an}的通项公式 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,$\frac{7}{2}$) | B. | [1,$\frac{7}{2}$] | C. | [-1,$\frac{7}{2}$] | D. | [-1,$\frac{7}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
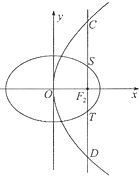 如图,椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的右焦点F2与抛物线y2=4x的焦点重合,过F2作与x轴垂直的直线l与椭圆交于S、T两点,与抛物线交于C、D两点,且$\frac{|CD|}{|ST|}=2\sqrt{2}$
如图,椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的右焦点F2与抛物线y2=4x的焦点重合,过F2作与x轴垂直的直线l与椭圆交于S、T两点,与抛物线交于C、D两点,且$\frac{|CD|}{|ST|}=2\sqrt{2}$查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com