
分析 (1)利用同角三角函数基本关系式可求cosC的值,利用三角形内角和定理,两角和的正弦函数公式即可计算求值sinA,进而利用正弦定理可求a的值.
(2)由余弦定理得AB,利用已知可求BD=1,在△BCD中由余弦定理得CD的值.
解答 解:(1)因为$sinC=\frac{{\sqrt{5}}}{5}$,则$cosC=\sqrt{1-{{sin}^2}C}=\sqrt{1-{{({\frac{{\sqrt{5}}}{5}})}^2}}=\frac{{2\sqrt{5}}}{5}$,…(1分)
所以:sinA=sin[π-(B+C)]=sin(B+C)=sinBcosC+cosBsinB
=$\frac{{\sqrt{2}}}{2}×\frac{{2\sqrt{5}}}{5}+\frac{{\sqrt{2}}}{2}×\frac{{\sqrt{5}}}{5}=\frac{{3\sqrt{10}}}{10}$,…(3分)
由正弦定理可得:$a=\frac{bsinA}{sinB}=\frac{{\sqrt{10}•\frac{{3\sqrt{10}}}{10}}}{{\frac{{\sqrt{2}}}{2}}}=3\sqrt{2}$…(6分)
(2)由余弦定理得${c^2}={({3\sqrt{2}})^2}+{({\sqrt{10}})^2}-2×({3\sqrt{2}})({\sqrt{10}})•\frac{{2\sqrt{5}}}{5}=4$,…(8分)
所以BD=1,
在△BCD中由余弦定理得CD2=BD2+BC2-2BD•BCcosB…(10分)
=$1+{({3\sqrt{2}})^2}-2×1×3\sqrt{2}\frac{{\sqrt{2}}}{2}=13$,
所以:$CD=\sqrt{13}$…(12分)
点评 本题主要考查了同角三角函数基本关系式,三角形内角和定理,两角和的正弦函数公式,正弦定理,余弦定理在解三角形中的综合应用,考查了计算能力和转化思想,属于中档题.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:高中数学 来源: 题型:选择题
 如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=$\frac{\sqrt{2}}{2}$,给出下列结论:
如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=$\frac{\sqrt{2}}{2}$,给出下列结论:| A. | 0个 | B. | 1 个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
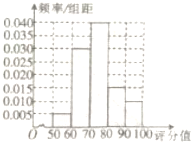 2015年11月11日,天猫交易额以912.17亿元的成绩刷新了世界纪录.随之快递的订单量也激增.某机构就双十一期间快递公司A的物流速度进行了随机调查,如图是200名受调查者对快递公司A的评分(百分制)的频率分布直方图,则其得分的众数大致为( )
2015年11月11日,天猫交易额以912.17亿元的成绩刷新了世界纪录.随之快递的订单量也激增.某机构就双十一期间快递公司A的物流速度进行了随机调查,如图是200名受调查者对快递公司A的评分(百分制)的频率分布直方图,则其得分的众数大致为( )| A. | 65 | B. | 70 | C. | 75 | D. | 80 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | $\sqrt{3}$ | C. | -$\sqrt{3}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,ln(ex-1)>0 | B. | ?x∈R,ln(ex-1)≥0 | C. | ?x∈R,ln(ex-1)<0 | D. | ?x∈R,ln(ex-1)≥0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com