
| A. | -3 | B. | $\sqrt{3}$ | C. | -$\sqrt{3}$ | D. | 3 |
分析 求出$\overrightarrow{e}$的坐标,代入投影公式计算即可.
解答 解:∵$\overrightarrow{e}$是与$\overrightarrow{b}$同向的单位向量,∴$\overrightarrow{e}$=($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),
∴$\overrightarrow{a}$在$\overrightarrow{e}$方向上的投影为|$\overrightarrow{a}$|•$\frac{\overrightarrow{a}•\overrightarrow{e}}{|\overrightarrow{a}||\overrightarrow{e}|}$=$\overrightarrow{a}•\overrightarrow{e}$=3.
故选D.
点评 本题考查了平面向量的数量积运算,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | {1} | B. | {-1,0} | C. | {0,1} | D. | {-1,0,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 PM2.5是指大气中直径≤2.5微米的颗粒物,其浓度是监测环境空气质量的重要指标.当PM2.5日均值在0~35(单位为微米/立方米,下同)时,空气质量为优,在35~75时空气质量为良,超过75时空气质量为污染.某旅游城市2016年春节7天假期里每天的PM2.5的监测数据如茎叶图所示.
PM2.5是指大气中直径≤2.5微米的颗粒物,其浓度是监测环境空气质量的重要指标.当PM2.5日均值在0~35(单位为微米/立方米,下同)时,空气质量为优,在35~75时空气质量为良,超过75时空气质量为污染.某旅游城市2016年春节7天假期里每天的PM2.5的监测数据如茎叶图所示.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
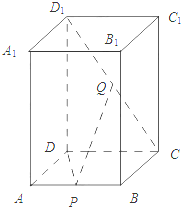 在四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD,底面ABCD为菱形,∠BAD=60°,P为AB的中点,Q为CD1的中点.
在四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD,底面ABCD为菱形,∠BAD=60°,P为AB的中点,Q为CD1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com