
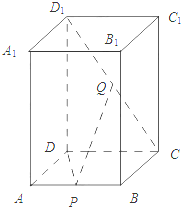
 在四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD,底面ABCD为菱形,∠BAD=60°,P为AB的中点,Q为CD1的中点.
在四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD,底面ABCD为菱形,∠BAD=60°,P为AB的中点,Q为CD1的中点.分析 (1)连结BD,推导出DP⊥AB,AA1⊥DP,由此能证明DP⊥平面A1ABB1.
(2)取CD中点M,推导出平面ADD1∥平面MPQ,由此能证明PQ∥平面ADD1A1.
(3)连结EB,推导出BE∥PQ,过B作BF∥AD,交PC于F,能推导出EF∥面DPQ.
解答 证明:(1)连结BD
∵在四棱柱ABCD-A1B1C1D1中,底面ABCD为菱形,∠BAD=60°,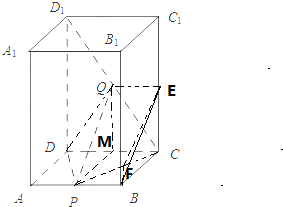
∴AP=AB=BD,
∵P为AB的中点,∴DP⊥AB,
∵AA1⊥平面ABCD,DP?平面ABCD,
∴AA1⊥DP,
∵AA1∩AB=A,∴DP⊥平面A1ABB1.
(2)取CD中点M,连结PM、QM,
∵P为AB的中点,Q为CD1的中点,
∴PM∥AD,QM∥DD1,
∵AD∩DD1=D,PM∩QM=M,
AD、DD1?平面ADD1,PM、QM?平面PQF,
∴平面ADD1∥平面MPQ,
∵PQ?平面PQF,∴PQ∥平面ADD1A1.
解:(3)连结EB,
∵Q为CD1的中点,E是CC1的中点,P为AB中点,∴QE$\underset{∥}{=}$PB,
∴四边形PBEQ是平行四边形,∴BE∥PQ,
过B作BF∥AD,交PC于F,
∵BE∥PQ,BF∥AD,BE∩BF=B,PQ∩PD=P,
BE、BF?平面BEF,PQ、PD?平面PDQ,
∴平面BEF∥平面PDQ,
∵EF?平面BEF,∴EF∥面DPQ.
点评 本题考查线面垂直和线面平行的证明,考查满足线面平行的点的确定与证明,是中档题,解题时要认真审题,注意空间思维能力的培养.


科目:高中数学 来源: 题型:填空题
 四个小动物换座位,开始是鼠、猴、兔、猫分别坐1、2、3、4号位上(如图),第一次前后排互换座位,第二次左右动物互换座位,…这样交替进行下去,那么202次互换座位后,小猴坐在第4号座位上.
四个小动物换座位,开始是鼠、猴、兔、猫分别坐1、2、3、4号位上(如图),第一次前后排互换座位,第二次左右动物互换座位,…这样交替进行下去,那么202次互换座位后,小猴坐在第4号座位上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | $\sqrt{3}$ | C. | -$\sqrt{3}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 13 | B. | 14 | C. | 15 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 0 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com