
分析 (1)当a=0时,利用函数奇偶性的定义进行判断即可;
(2)当x≤a时,f(x)=x2-x+a+1=(x-$\frac{1}{2}$)2+a+$\frac{3}{4}$,分a>$\frac{1}{2}$时和a≤$\frac{1}{2}$时两种情况,分别求得函数f(x)的最小值.
②当x>a 时,f(x)=x2+x-a+1=(x+$\frac{1}{2}$)2-a+$\frac{3}{4}$,分a>-$\frac{1}{2}$时和当a≤-$\frac{1}{2}$时两种情况,分别求得函数f(x)的最小值.
解答 解:(1)对于函数 f(x)=x2+|x-a|+1,
当a=0时,f(x)=x2+|x|+1为偶函数.
(2)①当x≤a时,f(x)=x2-x+a+1=(x-$\frac{1}{2}$)2+a+$\frac{3}{4}$,
若a>$\frac{1}{2}$时,函数f(x)的最小值为f($\frac{1}{2}$)=a+$\frac{3}{4}$;
若a≤$\frac{1}{2}$时,函数f(x)的最小值为f(a)=a2+1.
②当x>a 时,f(x)=x2+x-a+1=(x+$\frac{1}{2}$)2-a+$\frac{3}{4}$,
若a>-$\frac{1}{2}$时,函数f(x)的最小值为f(a)=a2+1;
若a≤-$\frac{1}{2}$时,函数f(x)的最小值为f(-$\frac{1}{2}$)=-a+$\frac{3}{4}$.
由a2+1>a+$\frac{3}{4}$,a2+1>-a+$\frac{3}{4}$,
综上可得,a>$\frac{1}{2}$时,函数f(x)的最小值为a+$\frac{3}{4}$;
a≤-$\frac{1}{2}$时,函数f(x)的最小值为-a+$\frac{3}{4}$;
当-$\frac{1}{2}$<a≤$\frac{1}{2}$,函数f(x)的最小值为a2+1.
点评 本题主要考查带有绝对值的函数,函数的奇偶性的判断,求二次函数的最值,体现了分类讨论的数学思想,属于中档题.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | $\sqrt{3}$ | C. | -$\sqrt{3}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
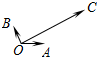 如图,平面内有三个向量$\overrightarrow{OA}$、$\overrightarrow{OB}$、$\overrightarrow{OC}$,其中$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为120°,$\overrightarrow{OA}$与$\overrightarrow{OC}$的夹角为30°,且|$\overrightarrow{OA}|=|\overrightarrow{OB}$|=1,|$\overrightarrow{OC}|=2\sqrt{3}$,若$\overrightarrow{OC}=x\overrightarrow{OA}+y\overrightarrow{OB}$(x,y∈R),则(x,y)=(4,2).
如图,平面内有三个向量$\overrightarrow{OA}$、$\overrightarrow{OB}$、$\overrightarrow{OC}$,其中$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为120°,$\overrightarrow{OA}$与$\overrightarrow{OC}$的夹角为30°,且|$\overrightarrow{OA}|=|\overrightarrow{OB}$|=1,|$\overrightarrow{OC}|=2\sqrt{3}$,若$\overrightarrow{OC}=x\overrightarrow{OA}+y\overrightarrow{OB}$(x,y∈R),则(x,y)=(4,2).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,ln(ex-1)>0 | B. | ?x∈R,ln(ex-1)≥0 | C. | ?x∈R,ln(ex-1)<0 | D. | ?x∈R,ln(ex-1)≥0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{8}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com