
分析 这是一个类比推理的题,在由平面图形到空间图形的类比推理中,一般是由点的性质类比推理到线的性质,由线的性质类比推理到面的性质,由已知在平面几何中在△ABC中,若∠C=90°,AC=b,BC=a,则△ABC的外接圆的半径r=$\frac{\sqrt{{a}^{2}+{b}^{2}}}{2}$,我们可以类比这一性质,推理出在空间中有三条侧棱两两垂直的四面体A-BCD中类似的结论.
解答 解:由已知在平面几何中,△ABC中,若∠C=90°,AC=b,BC=a,则△ABC的外接圆的半径r=$\frac{\sqrt{{a}^{2}+{b}^{2}}}{2}$,
我们可以类比这一性质,推理出:
取空间中有三条侧棱两两垂直的四面体A-BCD,且AB=a,AC=b,AD=c,则此三棱锥的外接球的半径是r=$\sqrt{\frac{{a}^{2}+{b}^{2}+{c}^{2}}{2}}$,
故答案为:$\sqrt{\frac{{a}^{2}+{b}^{2}+{c}^{2}}{2}}$.
点评 类比推理的一般步骤是:(1)找出两类事物之间的相似性或一致性;(2)用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(猜想).


 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | $\sqrt{3}$ | C. | -$\sqrt{3}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 13 | B. | 14 | C. | 15 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 0 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
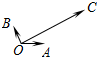 如图,平面内有三个向量$\overrightarrow{OA}$、$\overrightarrow{OB}$、$\overrightarrow{OC}$,其中$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为120°,$\overrightarrow{OA}$与$\overrightarrow{OC}$的夹角为30°,且|$\overrightarrow{OA}|=|\overrightarrow{OB}$|=1,|$\overrightarrow{OC}|=2\sqrt{3}$,若$\overrightarrow{OC}=x\overrightarrow{OA}+y\overrightarrow{OB}$(x,y∈R),则(x,y)=(4,2).
如图,平面内有三个向量$\overrightarrow{OA}$、$\overrightarrow{OB}$、$\overrightarrow{OC}$,其中$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为120°,$\overrightarrow{OA}$与$\overrightarrow{OC}$的夹角为30°,且|$\overrightarrow{OA}|=|\overrightarrow{OB}$|=1,|$\overrightarrow{OC}|=2\sqrt{3}$,若$\overrightarrow{OC}=x\overrightarrow{OA}+y\overrightarrow{OB}$(x,y∈R),则(x,y)=(4,2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com