
���� ��1������ֱ�ߺ�Բ���У����ݵ㵽ֱ�ߵľ�����ڰ뾶���������̽�����⼴�ɣ�
��2������|PQ|=$\frac{{\sqrt{2}}}{2}$|PO|���������̹�ϵ�������жϼ��ɣ�
��3������ֱ�ߺ�Բ�ཻ�����ʣ���������ε������ʽ������⼴�ɣ�
��� �⣺��1����Բ���ǣ�a��0������a��0��������ֱ��x-$\sqrt{3}$y+2=0�ľ�����d=$\frac{|a+2|}{\sqrt{1+3}}$=2��
���a=2��a=-6����ȥ�������ԣ�����ԲC�ķ����ǣ�x-2��2+y2=4����4�֣�
��2��������������ĵ�P��x��y��������$PA=\frac{{\sqrt{2}}}{2}PO$����x2+y2+4x+2=0����6�֣�
������P��ԲD����x+2��2+y2=2�ϣ���PҲ��ԲC����x-2��2+y2=4�ϣ�
��Ϊ$|{CD}|=4��{r_c}+{r_d}=2+\sqrt{2}$������ԲC��ԲD���룬ԲC��ԲDû�й����㣮
���ԣ������ڵ�P������������8�֣�
��3�����ڣ��������£���Ϊ��M��m��n������ԲC�ϣ����ԣ�m-2��2+n2=4��
��n2=4-��m-2��2=4m-m2��0��m��4��
��Ϊԭ�㵽ֱ��l��mx+ny=1�ľ���h=$\frac{1}{\sqrt{{m}^{2}+{n}^{2}}}$=$\frac{1}{\sqrt{4m}}$��1�����$\frac{1}{4}$��m��4 ��10�֣�
��|AB|=2$\sqrt{1-{h}^{2}}$��
����S��OAB=$\frac{1}{2}$|AB|h=$\sqrt{{h}^{2}-{h}^{4}}$=$\sqrt{\frac{1}{4m}-��\frac{1}{4m}��^{2}}$=$\sqrt{-��\frac{1}{4m}-\frac{1}{2}��^{2}+\frac{1}{4}}$��
��Ϊ$\frac{1}{16}��$$\frac{1}{4m}$��1�����Ե�$\frac{1}{4m}$=$\frac{1}{2}$����m=$\frac{1}{2}$ʱ��S��OABȡ�����ֵ$\frac{1}{2}$��
��ʱ��M�������ǣ�$\frac{1}{2}$��$\frac{\sqrt{7}}{2}$����$\frac{1}{2}$��-$\frac{\sqrt{7}}{2}$������OAB����������ֵ��$\frac{1}{2}$����12�֣�
���� ������Ҫ����ֱ�ߺ�Բ��λ�ù�ϵ��Ӧ�ã������������������ǽ������Ĺؼ�������ѧ���ļ���������


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0��x��1 | B�� | -1��x��1 | C�� | $\frac{1}{2}$��x��$\frac{2}{3}$ | D�� | $\frac{1}{2}$��x��2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-5��+�ޣ� | B�� | ��-5��-$\frac{3}{2}$�� | C�� | ��-$\frac{3}{2}$��1�� | D�� | ��-$\frac{3}{2}$��+�ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {1} | B�� | {-1��0} | C�� | {0��1} | D�� | {-1��0��1} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
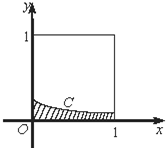 ����ͼ��ʾ�������������Ͷ��10 000���㣬��������Ӱ���֣�����CΪ��̬�ֲ�N��-1��1�����ܶ����ߣ��ĵ�ĸ����Ĺ���ֵΪ��������
����ͼ��ʾ�������������Ͷ��10 000���㣬��������Ӱ���֣�����CΪ��̬�ֲ�N��-1��1�����ܶ����ߣ��ĵ�ĸ����Ĺ���ֵΪ��������| A�� | 1 193 | B�� | 1 359 | C�� | 2 718 | D�� | 3 413 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com