
 如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=$\frac{\sqrt{2}}{2}$,给出下列结论:
如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=$\frac{\sqrt{2}}{2}$,给出下列结论:| A. | 0个 | B. | 1 个 | C. | 2个 | D. | 3个 |
分析 连结BD,则AC⊥平面BB1D1D,BD∥B1D1,由此能求出结果.找出两个特殊位置,即可判断(4)是不正确的;综合可得答案.
解答 解:连结BD,则AC⊥平面BB1D1D,BD∥B1D1,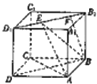
∴AC⊥BE,EF∥平面ABCD,三棱锥A-BEF的体积为定值,
从而(1)(2)(3)正确.
当点E在D1处,F为D1B1的中点时,异面直线AE,BF所成的角是∠FBC1,
当E在上底面的中心时,F在C1的位置,
异面直线AE,BF所成的角是∠EAA1
显然两个角不相等,(4)不正确.
故选:B.
点评 本题考查直线与平面垂直的判定,棱柱、棱锥、棱台的体积,异面直线及其所成的角,考查空间想象能力,逻辑思维能力,是中档题.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
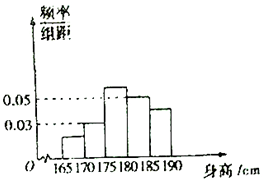 国防专业越来越受年轻学子的青睐,为了解某市高三报考国防专业学生的身高(单位:cm)情况,现将该市某学校报考国防专业的学生的身高作为样本,获得的数据整理后得到如图所示的频率分布直方图,其中样本数据的分组区间为[165,170),[170,175),[175,180),[180,185),[185,190).已知图中从左至右第一、三、五小组的频率之比为1:3:2,其中第三小组的频数为15.
国防专业越来越受年轻学子的青睐,为了解某市高三报考国防专业学生的身高(单位:cm)情况,现将该市某学校报考国防专业的学生的身高作为样本,获得的数据整理后得到如图所示的频率分布直方图,其中样本数据的分组区间为[165,170),[170,175),[175,180),[180,185),[185,190).已知图中从左至右第一、三、五小组的频率之比为1:3:2,其中第三小组的频数为15.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
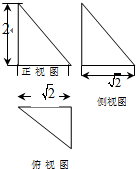
| A. | $\frac{8π}{3}$ | B. | 32π | C. | 8π | D. | 8$\sqrt{2}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1} | B. | {-1,0} | C. | {0,1} | D. | {-1,0,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 某校高三8个班,1班51人,2班53人,3班52人,由此推测各班人数都超过50人 | |
| B. | 由三角形的性质,推测空间四面体的性质 | |
| C. | 平行四边形的对角线互相平分,菱形是平行四边形,所以菱形的对角线互相平分 | |
| D. | 在数列{an}中,${a_1}=1,{a_n}=\frac{1}{2}({{a_{n-1}}+\frac{1}{{{a_{n-1}}}}})({n≥2})$,通过计算a2,a3,a4推理出{an}的通项公式 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com