
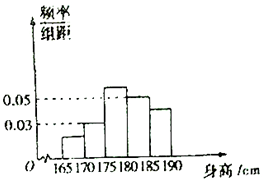
 国防专业越来越受年轻学子的青睐,为了解某市高三报考国防专业学生的身高(单位:cm)情况,现将该市某学校报考国防专业的学生的身高作为样本,获得的数据整理后得到如图所示的频率分布直方图,其中样本数据的分组区间为[165,170),[170,175),[175,180),[180,185),[185,190).已知图中从左至右第一、三、五小组的频率之比为1:3:2,其中第三小组的频数为15.
国防专业越来越受年轻学子的青睐,为了解某市高三报考国防专业学生的身高(单位:cm)情况,现将该市某学校报考国防专业的学生的身高作为样本,获得的数据整理后得到如图所示的频率分布直方图,其中样本数据的分组区间为[165,170),[170,175),[175,180),[180,185),[185,190).已知图中从左至右第一、三、五小组的频率之比为1:3:2,其中第三小组的频数为15.分析 (1)设从左至右第一、三、五小组的频率分别为p1,p2,p3,根据前3个小组的频率之比为1:3:2和所求频率和为1建立方程组,解之即可求出第二组频率,然后根求该校报考国防专业学生的总人数n即可;
(2)由1)可得,报考国防专业的学生的身高不低于175cm的概率p=p2+p3+0.05)×5=$\frac{3}{4}$,所以ξ服从二项分布B(4,$\frac{3}{4}$),从而求出ξ的分布列,最后利用数学期望公式进行求解.
解答 解:(1)设从左至右第一、三、五小组的频率分别为p1,p2,p3.
则由题意可知,$\left\{\begin{array}{l}{{p}_{2}=3{p}_{1}}\\{{p}_{3}=2{p}_{1}}\\{{p}_{1}+{p}_{2}+{p}_{3}+(0.03+0.05)×5=1}\end{array}\right.$.
解得p1=0.1,p2=0.3,p3=0.2.
因此该校报考国防专业的总人数n=$\frac{15}{0.3}$=50.
(2)由(1)可知,报考国防专业的学生的身高不低于175cm的概率p=p2+p3+0.05)×5=$\frac{3}{4}$.
所以ξ服从二项分布B(4,$\frac{3}{4}$),P(ξ=k)=${C}_{4}^{k}$( $\frac{3}{4}$)k•(1-$\frac{3}{4}$)4-k,k=0,1,2,3,4.
随机变量ξ的分布列为
| X | 0 | 1 | 2 | 3 | 4 |
| P | $\frac{1}{256}$ | $\frac{3}{64}$ | $\frac{27}{128}$ | $\frac{27}{64}$ | $\frac{81}{256}$ |
点评 本题主要考查了频率分布直方图,以及离散型随机变量的概率分布和数学期望,同时考查了计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 70 | B. | 80 | C. | 252 | D. | 126 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{12}$个单位长度而得到 | B. | 向右平移$\frac{π}{12}$个单位长度而得到 | ||
| C. | 向左平移$\frac{π}{4}$个单位长度而得到 | D. | 向右平移$\frac{π}{4}$个单位长度而得到 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=$\frac{\sqrt{2}}{2}$,给出下列结论:
如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=$\frac{\sqrt{2}}{2}$,给出下列结论:| A. | 0个 | B. | 1 个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
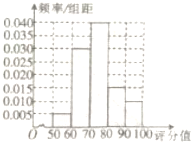 2015年11月11日,天猫交易额以912.17亿元的成绩刷新了世界纪录.随之快递的订单量也激增.某机构就双十一期间快递公司A的物流速度进行了随机调查,如图是200名受调查者对快递公司A的评分(百分制)的频率分布直方图,则其得分的众数大致为( )
2015年11月11日,天猫交易额以912.17亿元的成绩刷新了世界纪录.随之快递的订单量也激增.某机构就双十一期间快递公司A的物流速度进行了随机调查,如图是200名受调查者对快递公司A的评分(百分制)的频率分布直方图,则其得分的众数大致为( )| A. | 65 | B. | 70 | C. | 75 | D. | 80 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com