
分析 根据条件,利用待定系数法建立方程进行求解即可.
解答 解:设f(x)=ax+b,(a>0),
则由f(f(x))=16x+9,
得a(ax+b)+b=a2x+ab+b=16x+9,
则$\left\{\begin{array}{l}{{a}^{2}=16}\\{ab+b=9}\end{array}\right.$,得$\left\{\begin{array}{l}{a=4}\\{b=\frac{9}{5}}\end{array}\right.$,即f(x)=4x+$\frac{9}{5}$,
故答案为:4x+$\frac{9}{5}$
点评 本题主要考查函数解析式的求解,根据一次函数的定义,利用待定系数法是解决本题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
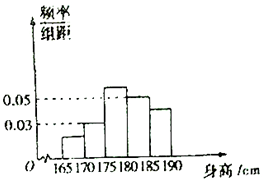 国防专业越来越受年轻学子的青睐,为了解某市高三报考国防专业学生的身高(单位:cm)情况,现将该市某学校报考国防专业的学生的身高作为样本,获得的数据整理后得到如图所示的频率分布直方图,其中样本数据的分组区间为[165,170),[170,175),[175,180),[180,185),[185,190).已知图中从左至右第一、三、五小组的频率之比为1:3:2,其中第三小组的频数为15.
国防专业越来越受年轻学子的青睐,为了解某市高三报考国防专业学生的身高(单位:cm)情况,现将该市某学校报考国防专业的学生的身高作为样本,获得的数据整理后得到如图所示的频率分布直方图,其中样本数据的分组区间为[165,170),[170,175),[175,180),[180,185),[185,190).已知图中从左至右第一、三、五小组的频率之比为1:3:2,其中第三小组的频数为15.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com