Question

10．已知函数f（x）=$\left\{\begin{array}{l}{a^x}，x≤1\\{x^2}-6x+8，x＞1\end{array}\right.$（a＞0，a≠1），若函数y=|f（x）|-a有三个零点，则实数a的取值范围是（1，3）．

Answer 1

分析 由题意可得函数y=|f（x）|的图象和直线y=a有3个交点，讨论0＜a＜1和1＜a＜3，a=3，a＞3，画出函数y=|f（x）|的图象，通过图象观察，即可得到所求a的范围．

解答 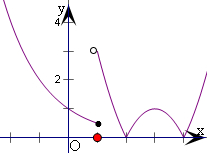解：函数y=|f（x）|-a有三个零点，
即为函数y=|f（x）|的图象和直线y=a有3个交点，
当0＜a＜1时，画出函数y=|f（x）|的图象，（如右图），
由x=1时，y=|f（1）|=a，即为直线y=a，
显然函数y=|f（x）|的图象和直线y=a有5个交点，不成立；
如右下图，
当1＜a＜3时，函数y=|f（x）|的图象和直线y=a有3个交点；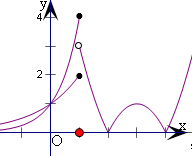
当a=3时，函数y=|f（x）|的图象和直线y=a有2个交点，
当a＞3时，函数y=|f（x）|的图象和直线y=a有2个交点．
综上可得，a的取值范围是（1，3）．
故答案为：（1，3）．

点评 本题考查函数零点的个数问题的解法，注意运用数形结合的思想方法，以及转化思想，转化为直线和曲线的交点是解题的关键，属于中档题．