
分析 (1)根据椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)短轴的两个顶点与右焦点的连线构成等边三角形,直线3x+4y+6=0与圆x2+(y-b)2=a2相切,建立方程组,求出a,b,即可求椭圆C的方程;
(2)由$\left\{\begin{array}{l}x=my-2\\{x^2}+4{y^2}-4=0\end{array}\right.$得(m2+4)y2-4my=0,求出M的坐标,同理可得N的坐标,分类讨论,即可证明结论;
(3)求出三角形的面积,变形,利用基本不等式求△AMN面积的最大值.
解答 解:(1)由题意$\left\{\begin{array}{l}a=2b\\ \frac{4b+6}{5}=a\end{array}\right.∴\left\{\begin{array}{l}a=2\\ b=1\end{array}\right.$即$C:\frac{x^2}{4}+{y^2}=1$…(4分)
(2)∵A(-2,0)设l1:x=my-2,${l_2}:x=-\frac{1}{m}y-2$
由$\left\{\begin{array}{l}x=my-2\\{x^2}+4{y^2}-4=0\end{array}\right.$得(m2+4)y2-4my=0∴$M(\frac{{2{m^2}-8}}{{{m^2}+4}},\frac{4m}{{{m^2}+4}})$
同理∴$N(\frac{{2-8{m^2}}}{{4{m^2}+1}},-\frac{4m}{{4{m^2}+1}})$(6分)
i) m≠±1时,${k_{MN}}=\frac{5m}{{4({m^2}-1)}}$${l_{MN}}:y=\frac{5m}{{4({m^2}-1)}}(x+\frac{6}{5})$过定点$(-\frac{6}{5},0)$
ii) m=±1时${l_{MN}}:x=-\frac{6}{5}$过点$(-\frac{6}{5},0)$∴lMN过定点$(-\frac{6}{5},0)$
(3)由(2)知${S_{△AMN}}=\frac{2}{5}|{\frac{4m}{{{m^2}+4}}+\frac{4m}{{4{m^2}+1}}}|=8|{\frac{{{m^3}+m}}{{4{m^4}+17{m^2}+4}}}|$
=$\frac{{8|{m+\frac{1}{m}}|}}{{4{{(m+\frac{1}{m})}^2}+9}}=\frac{8}{{4|{m+\frac{1}{m}}|+\frac{9}{{|{m+\frac{1}{m}}|}}}}$(8分)
令$t=|{m+\frac{1}{m}}|≥2且m=±1$时取等号,
∴${S_△}≤\frac{16}{25}且m=±1$时去等号,∴${S_{△max}}=\frac{16}{25}$(12分)
点评 本题考查了直线与椭圆的位置关系,联立方程组,结合韦达定理整体求解,属于难题.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
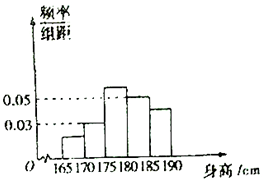 国防专业越来越受年轻学子的青睐,为了解某市高三报考国防专业学生的身高(单位:cm)情况,现将该市某学校报考国防专业的学生的身高作为样本,获得的数据整理后得到如图所示的频率分布直方图,其中样本数据的分组区间为[165,170),[170,175),[175,180),[180,185),[185,190).已知图中从左至右第一、三、五小组的频率之比为1:3:2,其中第三小组的频数为15.
国防专业越来越受年轻学子的青睐,为了解某市高三报考国防专业学生的身高(单位:cm)情况,现将该市某学校报考国防专业的学生的身高作为样本,获得的数据整理后得到如图所示的频率分布直方图,其中样本数据的分组区间为[165,170),[170,175),[175,180),[180,185),[185,190).已知图中从左至右第一、三、五小组的频率之比为1:3:2,其中第三小组的频数为15.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
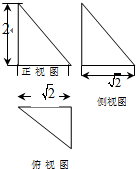
| A. | $\frac{8π}{3}$ | B. | 32π | C. | 8π | D. | 8$\sqrt{2}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1} | B. | {-1,0} | C. | {0,1} | D. | {-1,0,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com