
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
分析 令h(x)=0得出g(f(x))=1,设g(t)=1的解,作出f(x)的函数图象,根据图象判断f(x)=t的解得个数.
解答 解:令h(x)=0得g(f(x))=1,
令g(x)=1得$\left\{\begin{array}{l}{{e}^{x}=1}\\{x≤0}\end{array}\right.$或$\left\{\begin{array}{l}{|lnx|=1}\\{x>0}\end{array}\right.$,
解得x=0或x=e或x=$\frac{1}{e}$.
∴f(x)=0或f(x)=e或f(x)=$\frac{1}{e}$.
作出f(x)的函数图象如图所示: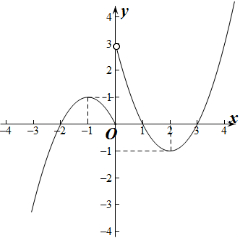
由图象可知f(x)=0有4个解,f(x)=e有两个解,f(x)=$\frac{1}{e}$有4个解,
∴h(x)共有10个零点.
故选:D.
点评 本题考查了复合函数的零点判断,二次函数的图象,属于中档题.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{1-x}$ | B. | $\frac{1}{(1-x)^{3}}$ | C. | -x | D. | x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
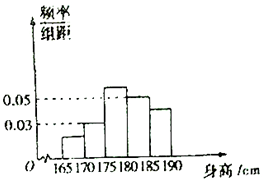 国防专业越来越受年轻学子的青睐,为了解某市高三报考国防专业学生的身高(单位:cm)情况,现将该市某学校报考国防专业的学生的身高作为样本,获得的数据整理后得到如图所示的频率分布直方图,其中样本数据的分组区间为[165,170),[170,175),[175,180),[180,185),[185,190).已知图中从左至右第一、三、五小组的频率之比为1:3:2,其中第三小组的频数为15.
国防专业越来越受年轻学子的青睐,为了解某市高三报考国防专业学生的身高(单位:cm)情况,现将该市某学校报考国防专业的学生的身高作为样本,获得的数据整理后得到如图所示的频率分布直方图,其中样本数据的分组区间为[165,170),[170,175),[175,180),[180,185),[185,190).已知图中从左至右第一、三、五小组的频率之比为1:3:2,其中第三小组的频数为15.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
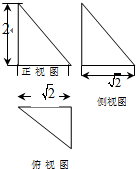
| A. | $\frac{8π}{3}$ | B. | 32π | C. | 8π | D. | 8$\sqrt{2}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
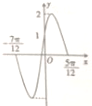
| A. | 2,2 | B. | 2,1 | C. | 4,2 | D. | 2,4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com