
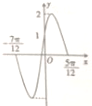
| A. | 2,2 | B. | 2,1 | C. | 4,2 | D. | 2,4 |
科目:高中数学 来源: 题型:选择题
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x≥-2} | B. | {x|-2<x<2} | C. | {x|-2≤x<2} | D. | {x|x<2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{13}{16}$ | B. | $\frac{4}{243}$ | C. | $\frac{13}{243}$ | D. | $\frac{80}{243}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
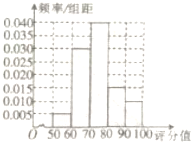 2015年11月11日,天猫交易额以912.17亿元的成绩刷新了世界纪录.随之快递的订单量也激增.某机构就双十一期间快递公司A的物流速度进行了随机调查,如图是200名受调查者对快递公司A的评分(百分制)的频率分布直方图,则其得分的众数大致为( )
2015年11月11日,天猫交易额以912.17亿元的成绩刷新了世界纪录.随之快递的订单量也激增.某机构就双十一期间快递公司A的物流速度进行了随机调查,如图是200名受调查者对快递公司A的评分(百分制)的频率分布直方图,则其得分的众数大致为( )| A. | 65 | B. | 70 | C. | 75 | D. | 80 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com