
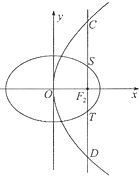
 如图,椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的右焦点F2与抛物线y2=4x的焦点重合,过F2作与x轴垂直的直线l与椭圆交于S、T两点,与抛物线交于C、D两点,且$\frac{|CD|}{|ST|}=2\sqrt{2}$
如图,椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的右焦点F2与抛物线y2=4x的焦点重合,过F2作与x轴垂直的直线l与椭圆交于S、T两点,与抛物线交于C、D两点,且$\frac{|CD|}{|ST|}=2\sqrt{2}$分析 (Ⅰ)由抛物线方程y2=4x得焦点F2(1,0),设椭圆E的方程为$\frac{{x}^{2}}{{b}^{2}+1}$+$\frac{{y}^{2}}{{b}^{2}}$=1,求出C(1,2),D(1,-2),由抛物线、椭圆都关于x轴对称,能求出椭圆方程.
(Ⅱ)设AB:y=k(x-2),由$\left\{\begin{array}{l}{y=k(x-2)}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$,得(1+2k2)x2-8k2x+8k2-2=0,由此利用根的判别式、韦达定理、向量知识、椭圆性质,结合已知条件能求出实数t的取值范围.
解答 解:(Ⅰ)∵椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的右焦点F2与抛物线y2=4x的焦点重合,
∴由抛物线方程y2=4x得焦点F2(1,0),
∴设椭圆E的方程为$\frac{{x}^{2}}{{b}^{2}+1}$+$\frac{{y}^{2}}{{b}^{2}}$=1,
解方程组$\left\{\begin{array}{l}{{y}^{2}=4x}\\{x=1}\end{array}\right.$,得C(1,2),D(1,-2),
∵抛物线、椭圆都关于x轴对称,
∴$\frac{|{F}_{2}C|}{|{F}_{2}S|}$=$\frac{|CD|}{|ST|}$=2$\sqrt{2}$,|F2S|=$\frac{\sqrt{2}}{2}$,∴S(1,$\frac{\sqrt{2}}{2}$),
∴$\frac{1}{{b}^{2}+1}$+$\frac{1}{2{b}^{2}}$=1,解得b2=1,
∴a2=1+1=2,
∴椭圆方程为$\frac{{x}^{2}}{2}+{y}^{2}=1$.
(Ⅱ)由题意知直线AB的斜率存在,
设AB:y=k(x-2),A(x1,y1),B(x2,y2),P(x,y),
由$\left\{\begin{array}{l}{y=k(x-2)}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$,得(1+2k2)x2-8k2x+8k2-2=0,
△=64k2-4(2k2+1)(8k2-2)>0,解得k2<$\frac{1}{2}$,
${x}_{1}+{x}_{2}=\frac{8{k}^{2}}{1+2{k}^{2}}$,${x}_{1}{x}_{2}=\frac{8{k}^{2}-2}{1+2{k}^{2}}$,
∵|AB|<$\frac{2\sqrt{5}}{3}$,
∴(1+k2)[$\frac{64{k}^{2}}{(1+2{k}^{2})^{2}}-4•\frac{8{k}^{2}-2}{1+2{k}^{2}}$]<$\frac{20}{9}$,
∴(4k2-1)(14k2+13)>0,∴k2>$\frac{1}{4}$,
∴$\frac{1}{4}<{k}^{2}<\frac{1}{2}$,
∵$\overrightarrow{OA}+\overrightarrow{OB}=t\overrightarrow{OP}$,∴(x1+x2,y1+y2)=t(x,y),
∴$x=\frac{{x}_{1}+{x}_{2}}{t}$,y=$\frac{{y}_{1}+{y}_{2}}{t}=\frac{1}{t}$[k(x1+x2)-4k]=$\frac{-4k}{t(1+2{k}^{2})}$,
∵点P在椭圆上,∴$\frac{(8{k}^{2})^{2}}{{t}^{2}(1+2{k}^{2})^{2}}$+2$•\frac{(-4k)^{2}}{{t}^{2}(1+2{k}^{2})^{2}}$=2,
∴16k2=t2(1+2k2),∴t2=$\frac{16{k}^{2}}{1+2{k}^{2}}$=8-$\frac{8}{1+2{k}^{2}}$,
∴$\frac{8}{3}<{t}^{2}<4$,
∴-2<t<-$\frac{2\sqrt{6}}{3}$或$\frac{2\sqrt{6}}{3}<t<2$,
∴实数t的取值范围为(-2,-$\frac{2\sqrt{6}}{3}$)∪($\frac{2\sqrt{6}}{3}$,2).
点评 本题考查椭圆方程的求法,考查实数的取值范围的求法,是中档题,解题时要认真审题,注意根的判别式、韦达定理、向量知识、椭圆性质的合理运用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
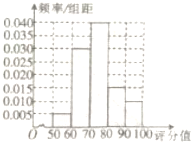 2015年11月11日,天猫交易额以912.17亿元的成绩刷新了世界纪录.随之快递的订单量也激增.某机构就双十一期间快递公司A的物流速度进行了随机调查,如图是200名受调查者对快递公司A的评分(百分制)的频率分布直方图,则其得分的众数大致为( )
2015年11月11日,天猫交易额以912.17亿元的成绩刷新了世界纪录.随之快递的订单量也激增.某机构就双十一期间快递公司A的物流速度进行了随机调查,如图是200名受调查者对快递公司A的评分(百分制)的频率分布直方图,则其得分的众数大致为( )| A. | 65 | B. | 70 | C. | 75 | D. | 80 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,ln(ex-1)>0 | B. | ?x∈R,ln(ex-1)≥0 | C. | ?x∈R,ln(ex-1)<0 | D. | ?x∈R,ln(ex-1)≥0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com