
���� ��1�����C��ֱ�����귽�̣�������C�ϵĵ㰴����任$\left\{\begin{array}{l}{x��=\frac{1}{3}x}\\{y��=\frac{1}{4}y}\end{array}\right.$�õ�����C��ķ��̣�
��2����ֱ��l�IJ�������Ϊ$\left\{\begin{array}{l}{x=-2+\frac{\sqrt{2}}{2}t}\\{y=\frac{\sqrt{2}}{2}t}\end{array}\right.$����y=$\frac{9}{4}$x2�У�������9t2-20$\sqrt{2}$t+72=0����A��B��Ӧ�IJ����ֱ�Ϊt1��t2����t�ü��������֪|MA||MB|=|t1t2|��
��� �⣺��1������C�ļ����귽���Ǧ�=$\frac{sin��}{1-si{n}^{2}��}$��ֱ�����귽��Ϊy=x2��
������C�ϵĵ㰴����任$\left\{\begin{array}{l}{x��=\frac{1}{3}x}\\{y��=\frac{1}{4}y}\end{array}\right.$�õ�����C��ķ���Ϊy=$\frac{9}{4}$x2��
��2����ֱ��l�IJ�������Ϊ$\left\{\begin{array}{l}{x=-2+\frac{\sqrt{2}}{2}t}\\{y=\frac{\sqrt{2}}{2}t}\end{array}\right.$����y=$\frac{9}{4}$x2�У�
������9t2-20$\sqrt{2}$t+72=0��
��A��B��Ӧ�IJ����ֱ�Ϊt1��t2��
��t1t2=9��
��t�ü��������֪��|MA|•|MB|=|t1t2|=9��
���� ���⿼���˼�������ֱ�����귽�̵Ļ�����ֱ�߷��������̵�Ӧ�ã�������������������������������е��⣮


 ��ѧʵ����ϵ�д�
��ѧʵ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
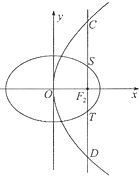 ��ͼ����ԲE��$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1��a��b��0�����ҽ���F2��������y2=4x�Ľ����غϣ���F2����x�ᴹֱ��ֱ��l����Բ����S��T���㣬�������߽���C��D���㣬��$\frac{|CD|}{|ST|}=2\sqrt{2}$
��ͼ����ԲE��$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1��a��b��0�����ҽ���F2��������y2=4x�Ľ����غϣ���F2����x�ᴹֱ��ֱ��l����Բ����S��T���㣬�������߽���C��D���㣬��$\frac{|CD|}{|ST|}=2\sqrt{2}$�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���ͦ£�m?��⇒m�ͦ� | B�� | ���ͦ£�m?����n?��⇒m��n | ||
| C�� | m��n��n�ͦ�⇒m�ͦ� | D�� | m?����n?����m�Φ£�n�Φ�⇒���Φ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 5 | C�� | $\sqrt{5}$ | D�� | $\sqrt{6}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com