
已知偶函数y=f(x)满足条件f(x+1)=f(x﹣1),且当x∈[﹣1,0]时,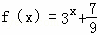 ,则
,则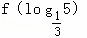 的值等于 .
的值等于 .
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
若数列{an}满足:存在正整数T,对于任意正整数n都有an+T=an成立,则称数列{an}为周期数列,周期为T.已知数列{an}满足a1=m(m>0),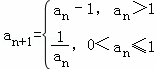 则下列结论中错误的是( )
则下列结论中错误的是( )
|
| A. | 若a3=4,则m可以取3个不同的值 |
|
| B. | 若 |
|
| C. | ∀T∈N*且T≥2,存在m>1,使得{an}是周期为T的数列 |
|
| D. | ∃m∈Q且m≥2,使得数列{an}是周期数列 |
查看答案和解析>>
科目:高中数学 来源: 题型:
函数f(x)的定义域为D,若对于任意x1,x2∈D,当x1<x2时,都有f(x1)≤f(x2),则称函数f(x)在D上为非减函数.设函数f(x)为定义在[0,1]上的非减函数,且满足以下三个条件:
①f(0)=0;②f(1﹣x)+f(x)=1x∈[0,1]; ③当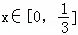 时,
时,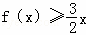 恒成立.则
恒成立.则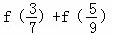 = .
= .
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=a•2|x|+1(a≠0),定义函数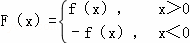 给出下列命题:
给出下列命题:
①F(x)=|f(x)|; ②函数F(x)是奇函数;③当a<0时,若mn<0,m+n>0,总有F(m)+F(n)<0成立,
其中所有正确命题的序号是( )
|
| A. | ② | B. | ①③ | C. | ②③ | D. | ①② |
查看答案和解析>>
科目:高中数学 来源: 题型:
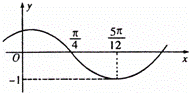
函数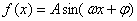 (其中A>0,|ω|<
(其中A>0,|ω|< )的图象如图所示,为得到
)的图象如图所示,为得到 的图象,则只要将
的图象,则只要将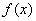 的图象( )A. 向右平移
的图象( )A. 向右平移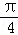 个单位长度 B. 向右平移
个单位长度 B. 向右平移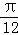 个单位长度
个单位长度
C. 向左平移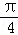 个单位长度 D. 向左平移
个单位长度 D. 向左平移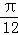 个单位长度
个单位长度
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com