
在三棱锥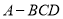 中,
中,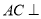 底面
底面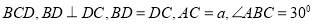 ,则点
,则点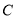 到平面
到平面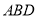 的距离是_____________。
的距离是_____________。
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源:2014-2015学年重庆市高一上学期第三次月考数学试卷(解析版) 题型:解答题
(本小题满分12分,(1)小问3分,(2)小问4分,(3)小问5分)
对于函数 ,若存在实数对(
,若存在实数对( ),使得等式
),使得等式 对定义域中的每一个
对定义域中的每一个 都成立,则称函数
都成立,则称函数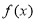 是“(
是“( )型函数”.
)型函数”.
(1)判断函数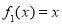 是否为 “(
是否为 “( )型函数”,并说明理由;
)型函数”,并说明理由;
(2)若函数 是“(
是“( )型函数”,求出满足条件的一组实数对
)型函数”,求出满足条件的一组实数对 ;
;
(3)已知函数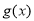 是“(
是“( )型函数”,对应的实数对
)型函数”,对应的实数对 为(1,4).当
为(1,4).当 时,
时,

 ,若当
,若当 时,都有
时,都有 ,试求
,试求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年重庆市高二上学期第三次月考理科数学试卷(解析版) 题型:解答题
(本小题13分)已知A为椭圆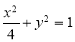 上的点,过A作AB
上的点,过A作AB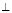 x轴,垂足为B,延长BA到C使得
x轴,垂足为B,延长BA到C使得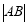 =
=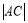 。
。
(1) 求点C的轨迹方程;
(2)直线l过点D (2,3)且与点C的轨迹只有一个交点,求l 的方程。
查看答案和解析>>
科目:高中数学 来源:2014-2015学年重庆市高二上学期第三次月考理科数学试卷(解析版) 题型:选择题
如图长方体中,AB=AD=2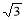 ,CC1=
,CC1=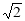 ,则二面角C1—BD—C的大小为( )
,则二面角C1—BD—C的大小为( )
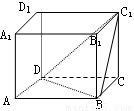
A.300 B.450 C.600 D.900
查看答案和解析>>
科目:高中数学 来源:2014-2015学年重庆市高二上学期第三次月考理科数学试卷(解析版) 题型:选择题
下列五个命题:
①若xy=0,则x=0且y=0”的逆否命题;
②正方形是菱形”的否命题;
③若 ”的逆命题;
”的逆命题;
④“m>2, ”;
”;
⑤命题p:“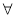
 ,
, ≥0”的否定是命题q:“
≥0”的否定是命题q:“
 ,
, ”,且命题q为假命题.
”,且命题q为假命题.
其中真命题的个数为( )
A.0个 B.1个 C.2个 D.3个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com