
【题目】已知函数![]() 为正常数.
为正常数.
⑴若![]() ,且
,且![]() ,求函数
,求函数![]() 的单调增区间;
的单调增区间;
⑵在⑴中当![]() 时,函数
时,函数![]() 的图象上任意不同的两点
的图象上任意不同的两点![]() ,线段
,线段![]() 的中点为
的中点为![]() ,记直线
,记直线![]() 的斜率为
的斜率为![]() ,试证明:
,试证明: ![]() .
.
⑶若![]() ,且对任意的
,且对任意的![]() ,
, ![]() ,都有
,都有![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)单调增区间为![]() . (2)见解析(3)
. (2)见解析(3)![]()
【解析】试题分析:(1)由题意先求出![]() 的解析式,然后求其导函数,令导函数大于
的解析式,然后求其导函数,令导函数大于![]() ,解出的即为函数的增区间;(2)对于当
,解出的即为函数的增区间;(2)对于当![]() 时,先求出
时,先求出![]() 的解析式,然后求导函数,得到
的解析式,然后求导函数,得到![]() ,在利用斜率公式求出过这两点的斜率公式,利用构造函数并利用构造函数的单调性比较大小;(3)因为
,在利用斜率公式求出过这两点的斜率公式,利用构造函数并利用构造函数的单调性比较大小;(3)因为![]() ,且对任意
,且对任意![]() ,都有
,都有![]() ,先写出
,先写出![]() 的解析式,利用该函数的单调性把问题转化为恒成立问题进行求解.
的解析式,利用该函数的单调性把问题转化为恒成立问题进行求解.
试题解析:⑴![]() ∵a
∵a![]() ,令
,令![]() 得x>3或0<x<
得x>3或0<x<![]() ,∴函数
,∴函数![]() 的单调增区间为
的单调增区间为![]() .
.
⑵证明:当![]() 时
时![]() ∴
∴![]() , ∴
, ∴![]() ,又
,又
不妨设![]() , 要比较
, 要比较![]() 与
与![]() 的大小,即比较
的大小,即比较![]() 与
与![]() 的大小,又∵
的大小,又∵![]() ,∴ 即比较
,∴ 即比较![]() 与
与![]() 的大小. 令
的大小. 令![]() ,则
,则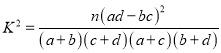 ,
,
∴![]() 在
在![]() 上位增函数.又
上位增函数.又![]() ,∴
,∴![]() , ∴
, ∴![]() ,即
,即![]()
⑶∵![]() ,∴
,∴ ![]() 由题意得
由题意得![]() 在区间
在区间![]() 上是减函数.
上是减函数.
![]() 当
当![]() , ∴
, ∴![]() 由
由![]() 在
在![]() 恒成立.设
恒成立.设![]() ,
, ![]() ,则
,则![]() ∴
∴![]() 在
在![]() 上为增函数,∴
上为增函数,∴![]() .
.
当![]() ,∴
,∴ ![]() 由
由
![]() 在
在![]() 恒成立
恒成立
设![]()
![]() ,
, ![]() 为增函数,∴
为增函数,∴![]() 综上:a的取值范围为
综上:a的取值范围为![]()


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:
【题目】(本小题满分14分)
已知函数![]() (
(![]() 为常数)的图像与
为常数)的图像与![]() 轴交于点
轴交于点![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线斜率为
处的切线斜率为![]() .
.
(1)求![]() 的值及函数
的值及函数![]() 的极值;
的极值;
(2)证明:当![]() 时,
时,![]()
(3)证明:对任意给定的正数![]() ,总存在
,总存在![]() ,使得当
,使得当![]() 时,恒有
时,恒有![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)的定义域为(-3,3),
满足f(-x)=-f(x),且对任意x,y,都有f(x)-f(y)=f(x-y),当x<0时,f(x)>0,f(1)=-2.
(1)求f(2)的值;
(2)判断f(x)的单调性,并证明;
(3)若函数g(x)=f(x-1)+f(3-2x),求不等式g(x)≤0的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn,![]() ,Sn=n2an-n(n-1),n=1,2,…
,Sn=n2an-n(n-1),n=1,2,…
(1)证明:数列{![]() Sn}是等差数列,并求Sn;
Sn}是等差数列,并求Sn;
(2)设![]() ,求证 :b1+b2+…+bn<1.
,求证 :b1+b2+…+bn<1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com