
【题目】2017年春晚分会场之一是凉山西昌,电视播出后,通过网络对凉山分会场的表演进行了调查.调查分三类人群进行,参加了网络调查的观众们的看法情况如下:
观众对凉山分会场表演的看法 | 非常好 | 好 |
中国人且非四川(人数比例) |
|
|
四川人(非凉山)(人数比例) |
|
|
凉山人(人数比例) |
|
|
(1)从这三类人群中各选一个人,求恰好有2人认为“非常好”的概率(用比例作为相应概率);
(2)若在四川人(非凉山)群中按所持态度分层抽样,抽取9人,在这9人中任意选取3人,认为“非常好”的人数记为ξ,求ξ的分布列和数学期望.
【答案】
(1)解:设事件“恰好有2人认为“非常好””为A,则P(A)= ![]() ×
× ![]() ×
× ![]() +
+ ![]() ×
× ![]() ×
× ![]() +
+ ![]() ×
× ![]() ×
× ![]() =
= ![]() .
.
(2)解:若在四川人(非凉山)群中按所持态度分层抽样,抽取9人,则其中认为“非常好”的人数为6,认为“好”的人数为3.在这9人中任意选取3人,认为“非常好”的人数记为ξ,则ξ的可能取值为:0,1,2,3.
P(ξ=0)= ![]() =
= ![]() ,P(ξ=1)=
,P(ξ=1)= ![]() =
= ![]() ,P(ξ=2)=
,P(ξ=2)= ![]() =
= ![]() ,P(ξ=3)=
,P(ξ=3)= ![]() =
= ![]() .
.
∴ξ的分布列为:
ξ | 0 | 1 | 2 | 3 |
P |
|
|
|
|
E(ξ)=0× ![]() +1×
+1× ![]() +2×
+2× ![]() +3×
+3× ![]() =2.
=2.
【解析】(1)设事件“恰好有2人认为“非常好””为A,利用互相独立与互斥事件的概率计算公式即可得出.(2)若在四川人(非凉山)群中按所持态度分层抽样,抽取9人,则其中认为“非常好”的人数为6,认为“好”的人数为3.在这9人中任意选取3人,认为“非常好”的人数记为ξ,则ξ的可能取值为:0,1,2,3.利用“超几何分布列”的概率计算公式及其数学期望计算公式即可得出.
【考点精析】通过灵活运用离散型随机变量及其分布列,掌握在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列即可以解答此题.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)= 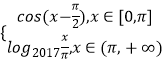 ,若有三个不同的实数a,b,c,使得f(a)=f(b)=f(c),则a+b+c的取值范围为( )
,若有三个不同的实数a,b,c,使得f(a)=f(b)=f(c),则a+b+c的取值范围为( )
A.(2π,2017π)
B.(2π,2018π)
C.( ![]() ,
, ![]() )
)
D.(π,2017π)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义[x]表示不超过x的最大整数,例如[2.11]=2,[﹣1.39]=﹣2,执行如下图所示的程序框图,则输出m的值为 ( )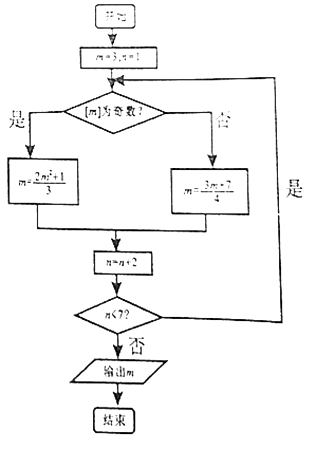
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是等差数列,数列{bn}是等比数列,Sn是数列{an}的前n项和,a1=b1=1,S2=![]() .
.
(1)若b2是a1,a3的等差中项,求数列{an}与{bn}的通项公式;
(2)若an∈N+,数列{![]() }是公比为9的等比数列,求证:
}是公比为9的等比数列,求证:![]() +
+![]() +
+![]() +…+
+…+![]() <
<![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点M到点
中,点M到点![]() 的距离比它到
的距离比它到![]() 轴的距离大2,记点M的轨迹为C.
轴的距离大2,记点M的轨迹为C.
(1)求轨迹C的方程;
(2)若直线![]() 与轨迹C恰有2个公共点,求实数b的取值范围.
与轨迹C恰有2个公共点,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,其中m,n,k∈R.
,其中m,n,k∈R.
(1)若m=n=k=1,求f(x)的单调区间;
(2)若n=k=1,且当x≥0时,f(x)≥1总成立,求实数m的取值范围;
(3)若m>0,n=0,k=1,若f(x)存在两个极值点x1、x2 , 求证: ![]() <f(x1)+f(x2)<
<f(x1)+f(x2)< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线y2=2px(p>0)的焦点为F,A(x1,y1),B(x2,y2)是过F的直线与抛物线的两个交点,求证:
(1)y1y2=-p2,![]() ;(2)
;(2)![]() 为定值;
为定值;
(3)以AB为直径的圆与抛物线的准线相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=aex﹣x(a∈R),其中e为自然对数的底数,e=2.71828…
(Ⅰ)判断函数f(x)的单调性,并说明理由
(Ⅱ)若x∈[1,2],不等式f(x)≥e﹣x恒成立,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com