
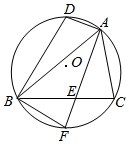
 如图所示,△ABC内接于圆O,D是$\widehat{BAC}$的中点,∠BAC的平分线分别交BC和圆O于点E,F.
如图所示,△ABC内接于圆O,D是$\widehat{BAC}$的中点,∠BAC的平分线分别交BC和圆O于点E,F.分析 (Ⅰ)设△ABE外接圆的圆心为O′,连结BO′并延长交圆O′于G点,连结GE,则∠BEG=90°,∠BAE=∠BGE,可证∠FBE=∠BAE,进而证明∠FBG=90°,即可得证BF是△ABE外接圆的切线.
(Ⅱ)连接DF,则DF⊥BC,由勾股定理可得BD2-DA2=AF2-BF2,利用相似三角形的性质可得AB•AC=AE•AF=(AF-EF)•AF,由△FBE∽△FAB,从而BF2=FE•FA,得AB-AC=AF2-BF2,进而可求BD2-DA2=AB•AC=6.
解答  (本题满分为10分).
(本题满分为10分).
解:(Ⅰ)设△ABE外接圆的圆心为O′,连结BO′并延长交圆O′于G点,连结GE,
则∠BEG=90°,∠BAE=∠BGE.
因为AF平分∠BAC,
所以$\widehat{BF}=\widehat{FC}$,
所以∠FBE=∠BAE,(2分)
所以∠FBG=∠FBE+∠EBG=∠BGE+∠EBG=180°-∠BEG=90°,
所以O′B⊥BF,
所以BF是△ABE外接圆的切线…(5分)
(Ⅱ)连接DF,则DF⊥BC,
所以DF是圆O的直径,
因为BD2+BF2=DF2,DA2+AF2=DF2,
所以BD2-DA2=AF2-BF2.(7分)
因为AF平分∠BAC,
所以△ABF∽△AEC,
所以$\frac{AB}{AE}$=$\frac{AF}{AC}$,
所以AB•AC=AE•AF=(AF-EF)•AF,
因为∠FBE=∠BAE,
所以△FBE∽△FAB,从而BF2=FE•FA,
所以AB-AC=AF2-BF2,
所以BD2-DA2=AB•AC=6…(10分)
点评 本小题主要考查圆周角定理、相似三角形的判定与性质、切割线定理等基础知识,考查推理论证能力、运算求解能力等,考查化归与转化思想等,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,三棱锥P-ABC中,PA⊥平面ABC,PA=$\sqrt{2}$,AC⊥BC,AC=BC=2,D在棱PB上,且PD=λPB(0<λ<1).
如图,三棱锥P-ABC中,PA⊥平面ABC,PA=$\sqrt{2}$,AC⊥BC,AC=BC=2,D在棱PB上,且PD=λPB(0<λ<1).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
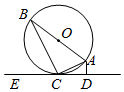 如图,半径为$\frac{9}{2}$的△ABC的外接圆圆O的直径为AB,直线CE为圆O的切线且相切于点C,AD⊥CE于点D,AD=1.
如图,半径为$\frac{9}{2}$的△ABC的外接圆圆O的直径为AB,直线CE为圆O的切线且相切于点C,AD⊥CE于点D,AD=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
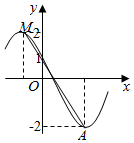 已知f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,|MN|=5,则f(x)=2sin($\frac{π}{3}$x+$\frac{π}{6}$).
已知f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,|MN|=5,则f(x)=2sin($\frac{π}{3}$x+$\frac{π}{6}$).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com