
 如图,三棱锥P-ABC中,PA⊥平面ABC,PA=$\sqrt{2}$,AC⊥BC,AC=BC=2,D在棱PB上,且PD=λPB(0<λ<1).
如图,三棱锥P-ABC中,PA⊥平面ABC,PA=$\sqrt{2}$,AC⊥BC,AC=BC=2,D在棱PB上,且PD=λPB(0<λ<1).分析 (Ⅰ)建立空间坐标系,求出AD和PC对应的向量,利用直线垂直和向量数量积的关系,利用向量法建立方程关系即可求λ的值;
(Ⅱ)在(Ⅰ)的条件下,求出平面的法向量先求出二面角的余弦值即可求二面角B-AD-C的正弦值.
解答  解:(Ⅰ)建立以O为坐标原点,OB,OA,OD分别为x,y,z轴的空间直角坐标系如图:
解:(Ⅰ)建立以O为坐标原点,OB,OA,OD分别为x,y,z轴的空间直角坐标系如图:
则A(0,0,0),B(2,2,0),C(0,2,0),P(0,0,$\sqrt{2}$),
则$\overrightarrow{PB}$=(2,2,-$\sqrt{2}$),$\overrightarrow{PC}$=(0,2,-$\sqrt{2}$),$\overrightarrow{AP}$=(0,0,$\sqrt{2}$),
∵PD=λPB,∴$\overrightarrow{PD}$=λ$\overrightarrow{PB}$=(2λ,2λ,-$\sqrt{2}$λ),
则$\overrightarrow{AD}$=$\overrightarrow{AP}$+$\overrightarrow{PD}$=(2λ,2λ,$\sqrt{2}$-$\sqrt{2}$λ),
∵AD⊥PC,∴$\overrightarrow{AD}$•$\overrightarrow{PC}$=0,即(2λ,2λ,$\sqrt{2}$-$\sqrt{2}$λ)•(0,2,-$\sqrt{2}$)=4λ-2+2λ=0,
得λ=$\frac{1}{3}$.
(Ⅱ)∵λ=$\frac{1}{3}$,∴$\overrightarrow{AD}$=(2λ,2λ,$\sqrt{2}$-$\sqrt{2}$λ)=($\frac{2}{3}$,$\frac{2}{3}$,$\frac{2\sqrt{2}}{3}$),则D($\frac{2}{3}$,$\frac{2}{3}$,$\frac{2\sqrt{2}}{3}$),
设面CAD的法向量为$\overrightarrow{m}$=(x,y,z),
则$\overrightarrow{AD}$=($\frac{2}{3}$,$\frac{2}{3}$,$\frac{2\sqrt{2}}{3}$),$\overrightarrow{DC}$=(0,2,0),
即$\overrightarrow{m}$•$\overrightarrow{AD}$=$\frac{2}{3}$x+$\frac{2}{3}$y+$\frac{2\sqrt{2}}{3}$z=0,$\overrightarrow{m}$•$\overrightarrow{DC}$=2y=0,
设x=1,则$\overrightarrow{m}$=(1,0,-$\frac{\sqrt{2}}{2}$),
取AB的中点O,连接OC,
∵AC=BC=2,∴CO⊥AB,
∵PA⊥平面PAB,
∴平面PAB的一个法向量为$\overrightarrow{n}$=$\overrightarrow{OC}$=(-1,1,0)
$cos<\overrightarrow{m},\overrightarrow{n}>$=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{-1}{\sqrt{2}•\sqrt{\frac{3}{2}}}$=$-\frac{\sqrt{3}}{3}$,
则sin<$\overrightarrow{m}$,$\overrightarrow{n}$>=$\frac{\sqrt{6}}{3}$,
即二面角B-AD-C的正弦值是$\frac{\sqrt{6}}{3}$.
点评 本题主要考查空间直线垂直及二面角的求解,建立坐标系,求出平面的法向量,利用向量法是解决本题的关键.综合考查学生的运算和推理能力.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:填空题
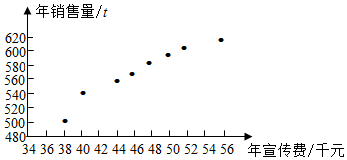 某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响.对近8年的年宣传费xi和年销售量yi(i=1,2,…,8)数据作了初步处理,得到如图所示的散点图及一些统计量的值.
某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响.对近8年的年宣传费xi和年销售量yi(i=1,2,…,8)数据作了初步处理,得到如图所示的散点图及一些统计量的值.| $\overline{x}$ | $\overline{y}$ | $\overline{w}$ | $\sum_{i=1}^{8}$(xi-$\overline{x}$)2 | $\sum_{i=1}^{8}({w}_{i}-\overline{w})^{2}$ | $\sum_{i=1}^{8}$(xi-$\overline{x}$)(y1-$\overline{y}$) | $\sum_{i=1}^{8}$(wi-$\overline{w}$)(yi-$\overline{y}$) |
| 46.6 | 563 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{x\sqrt{x}}$ | B. | -$\frac{1}{x\sqrt{x}}$ | C. | -$\frac{2}{x\sqrt{x}}$ | D. | -$\frac{2}{{x}^{2}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
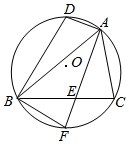 如图所示,△ABC内接于圆O,D是$\widehat{BAC}$的中点,∠BAC的平分线分别交BC和圆O于点E,F.
如图所示,△ABC内接于圆O,D是$\widehat{BAC}$的中点,∠BAC的平分线分别交BC和圆O于点E,F.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | π | D. | $\frac{4π}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com