
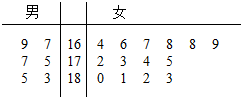
 某航空公司在2015年年初招收了20名空乘人员(服务员与空警),其中“男性空乘人员”5名,“女性空乘人员”14名,并对他们的身高进行了测量,其身高(单位:cm)的茎叶图如图所示.
某航空公司在2015年年初招收了20名空乘人员(服务员与空警),其中“男性空乘人员”5名,“女性空乘人员”14名,并对他们的身高进行了测量,其身高(单位:cm)的茎叶图如图所示.分析 (1)由茎叶图把14名“女性空乘人员”从低到高排列,找出身高位于中间位置的两位数是172和173,由此能求出“女性空乘人员”身高的中位数,先求出“男性空乘人员”身高的平均数,再求出“男性空乘人员”身高的方差.
(2)由茎叶图知,6名“男性空乘人员”中2人进入“国内航班”做空乘人员,4人“国际航班”做空乘人员,14名“女性空乘人员”中6人进入“国内航班”做空乘人员,8人“国际航班”做空乘人员,X的可能取值为0,1,2,3,分别求出相应的概率,由此能求出X的分布列和EX.
解答 解:(1)由茎叶图知,14名“女性空乘人员”从低到高排列,身高位于中间位置的两位数是172和173,
∴“女性空乘人员”身高的中位数为:$\frac{172+173}{2}$=172.5(cm).
“男性空乘人员”身高的平均数为:$\overline{x}$=175+$\frac{-8-6+0+2+8+10}{6}$=176(cm),
∴“男性空乘人员”身高的方差:
S2=$\frac{1}{6}$[(167-176)2+(169-176)2+(175-176)2+(177-176)2+(183-176)2+(185-176)2]≈43.67.
(2)由茎叶图知,6名“男性空乘人员”中2人进入“国内航班”做空乘人员,4人“国际航班”做空乘人员,
14名“女性空乘人员”中6人进入“国内航班”做空乘人员,8人“国际航班”做空乘人员,
∴X的可能取值为0,1,2,3,
P(X=0)=$\frac{{C}_{2}^{2}}{{C}_{6}^{2}}•\frac{{C}_{6}^{1}}{{C}_{14}^{1}}$=$\frac{6}{210}$,
P(X=1)=$\frac{{C}_{2}^{1}{C}_{4}^{1}}{{C}_{6}^{2}}•\frac{{C}_{6}^{1}}{{C}_{14}^{1}}+\frac{{C}_{2}^{2}}{{C}_{6}^{2}}•\frac{{C}_{8}^{1}}{{C}_{14}^{1}}$=$\frac{56}{210}$,
P(X=2)=$\frac{{C}_{2}^{1}{C}_{4}^{1}}{{C}_{6}^{2}}•\frac{{C}_{8}^{1}}{{C}_{14}^{1}}+\frac{{C}_{4}^{2}}{{C}_{6}^{2}}•\frac{{C}_{6}^{1}}{{C}_{8}^{1}}$=$\frac{100}{210}$,
P(X=3)=$\frac{{C}_{4}^{2}}{{C}_{6}^{2}}•\frac{{C}_{8}^{1}}{{C}_{14}^{1}}$=$\frac{48}{210}$,
∴X的分布列为:
| X | 0 | 1 | 2 | 3 |
| P | $\frac{6}{210}$ | $\frac{56}{210}$ | $\frac{100}{210}$ | $\frac{48}{210}$ |
点评 本题考查中位数、方差的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意茎叶图性质的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | 在β内必存在与a平行的直线 | B. | 在β内必存在与a垂直的直线 | ||
| C. | 在β内不存在与a平行的直线 | D. | 在β内不一定存在与a垂直的直线 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ${C}_{8}^{4}$${A}_{4}^{4}$ | B. | ${C}_{8}^{4}$${A}_{4}^{4}$${C}_{5}^{1}$ | C. | 54${C}_{8}^{4}$${A}_{4}^{4}$ | D. | ${C}_{40}^{4}$${A}_{4}^{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com