
分析 由条件利用诱导公式化简所给的三角函数式的值,可得结果.
解答 解:(1)sin(-1740°)cos1470°+cos(-660°)sin750°+tan405°
=sin(-5×360°+60°)cos(360°×4+30°)+cos(-720°+60°)sin(72°+30°)+tan(360°+45°)
=sin60°cos30°+cos60°sin30°+tan45°
=sin(60°+30°)+1=2.
(2)$sin{\;}^2\frac{17π}{4}+tan{\;}^2\frac{11π}{6}tan\frac{9π}{4}$=sin2$\frac{π}{4}$+${tan}^{2}(-\frac{π}{6})$•tan$\frac{π}{4}$=$\frac{1}{2}$+$\frac{1}{3}$•1=$\frac{5}{6}$.
点评 本题主要考查应用诱导公式化简三角函数式,要特别注意符号的选取,这是解题的易错点,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | (3,4) | C. | (1,3) | D. | (1,2)∪(3,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | k≥1 | B. | k≥$\frac{3}{4}$ | C. | k≤1 | D. | k≤$\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
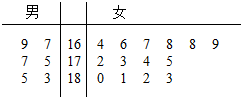 某航空公司在2015年年初招收了20名空乘人员(服务员与空警),其中“男性空乘人员”5名,“女性空乘人员”14名,并对他们的身高进行了测量,其身高(单位:cm)的茎叶图如图所示.
某航空公司在2015年年初招收了20名空乘人员(服务员与空警),其中“男性空乘人员”5名,“女性空乘人员”14名,并对他们的身高进行了测量,其身高(单位:cm)的茎叶图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
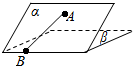 如图,二面角α-l-β的大小是30°,线段AB?α,B∈l,AB与l所成的角为30°.则AB与平面β所成的角的正弦值是$\frac{1}{4}$.
如图,二面角α-l-β的大小是30°,线段AB?α,B∈l,AB与l所成的角为30°.则AB与平面β所成的角的正弦值是$\frac{1}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com