
分析 (Ⅰ)利用代入法求椭圆方程;
(Ⅱ)设A(x1,y1),B(x2,y2),由直线代入椭圆方程,消去y,得(1+4k2)x2+8kmx+4m2-4=0,由此利用根的判别式、韦达定理、中点坐标公式,结合已知条件能证明结论.
解答 解:(Ⅰ)设点F(x,y),点P(x',y'),因为点P在x轴上的射影为H,所以H(x',0).
又因为$\overrightarrow{OH}+\overrightarrow{OP}=2\overrightarrow{OF}$,所以点F是线段PH的中点,
即有$\left\{\begin{array}{l}x=x'\\ y=\frac{y'}{2}\end{array}\right.⇒\left\{\begin{array}{l}x'=x\\ y'=2y\end{array}\right.$…(3分)
因为点P是圆x2+y2=4上任意一点,所以(x')2+(y')2=4,
所以${(x)^2}+{({2y})^2}=4⇒\frac{x^2}{4}+{y^2}=1$.
所以点F的轨迹C的方程为$\frac{x^2}{4}+{y^2}=1$…(5分)
(Ⅱ)设A(x1,y1),B(x2,y2),联立解方程组:$\left\{\begin{array}{l}y=kx+m\\ \frac{x^2}{4}+{y^2}=1\end{array}\right.⇒({1+4{k^2}}){x^2}+8kmx+4{m^2}-4=0$,…(7分)
∴$\left\{\begin{array}{l}△={({8km})^2}-4({1+4{k^2}})({4{m^2}-4})>0\\{x_1}+{x_2}=\frac{-8km}{{1+4{k^2}}}\\{x_1}{x_2}=\frac{{4{m^2}-4}}{{1+4{k^2}}}\end{array}\right.$,即$\left\{\begin{array}{l}{m^2}<1+4{k^2}\\{x_1}+{x_2}=\frac{-8km}{{1+4{k^2}}}\\{x_1}{x_2}=\frac{{4{m^2}-4}}{{1+4{k^2}}}\end{array}\right.$,…(9分)
∴${y_1}+{y_2}=k({x_1}+{x_2})+2m=\frac{2m}{{1+4{k^2}}}$.
又点N是线段AB中点,由中点坐标公式,得$N(\frac{-4km}{{1+4{k^2}}},\frac{m}{{1+4{k^2}}})$,…(10分)
又$\overrightarrow{OQ}=\sqrt{2}\overrightarrow{ON}$,得$Q(\frac{{-4\sqrt{2}km}}{{1+4{k^2}}},\frac{{\sqrt{2}m}}{{1+4{k^2}}})$,…(11分)
将$Q(\frac{{-4\sqrt{2}km}}{{1+4{k^2}}},\frac{{\sqrt{2}m}}{{1+4{k^2}}})$代入椭圆方程$\frac{x^2}{4}+{y^2}=1$,
得$\frac{{8{k^2}{m^2}}}{{{{({1+4{k^2}})}^2}}}+\frac{{2{m^2}}}{{{{({1+4{k^2}})}^2}}}=1$,化简得2m2=16k4+8k2+1-8k2m2…(13分)
点评 本题考查椭圆方程的求法,考查方程的证明,考查三角形面积的求法,解题时要认真审题,注意弦长公式的合理运用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
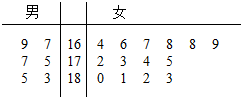 某航空公司在2015年年初招收了20名空乘人员(服务员与空警),其中“男性空乘人员”5名,“女性空乘人员”14名,并对他们的身高进行了测量,其身高(单位:cm)的茎叶图如图所示.
某航空公司在2015年年初招收了20名空乘人员(服务员与空警),其中“男性空乘人员”5名,“女性空乘人员”14名,并对他们的身高进行了测量,其身高(单位:cm)的茎叶图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{2}$) | B. | ($\frac{1}{2},1$) | C. | (-1,$\frac{1}{2}$) | D. | (0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 2$\sqrt{2}$ | C. | 4 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 直径/mm | 58 | 59 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 73 | 合计 |
| 件数 | 1 | 1 | 3 | 5 | 6 | 19 | 33 | 18 | 4 | 4 | 2 | 1 | 2 | 1 | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | -3 | C. | $\sqrt{3}$ | D. | -3$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com