练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知函数f（x）=log2（
    		1+25x2
    -5x）+3，则f（lna）+f（ln
    1
    a
    ）的值（　　）
    A、为-6B、为6
    C、为0D、与a的取值有关
    考点：函数的值
    专题：函数的性质及应用
    分析：根据题意，设g（x）=log2（
    		1+25x2
    -5x），x∈R，得出g（x）是奇函数；由ln
    1
    a
    =-lna，计算f（lna）+f（ln
    1
    a
    ）即可．
    解答： 解：根据题意，设g（x）=log2（
    		1+25x2
    -5x），x∈R；
    ∴g（-x）=log2（
    		1+25x2
    +5x）
    =log2
    1
    		1+25x2
    -5x

    =-log2（
    		1+25x2
    -5x）
    =-g（x）；
    ∴g（x）是定义域R上的奇函数；
    ∴f（x）=g（x）+3；
    又∵ln
    1
    a
    =-lna，
    ∴f（lna）+f（ln
    1
    a
    ）=f（lna）+f（-lna）
    =[g（lna）+3]+[g（-lna）+3]
    =[g（lna）+g（-lna）]+6
    =6．
    故选：B．
    点评：本题考查了函数的奇偶性的应用问题，解题时应根据函数的奇偶性，灵活地利用g（lna）+g（-lna）=0这一结论，是基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    设实系数一元二次方程x2+ax+2b-2=0有两相异实根，其中一根在区间（0，1）内，另一根在区间（1，2）内，则
    2b-8
    a-1
    的取值范围是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    定义：若数列{an}对n∈N*，都有|an+1|+|an|=d（d为常数），则称{an}为“绝对和数列”，d叫做“绝对公和”，已知“绝对和数列”{an}中，a1=1，绝对公和为3，则{an}的前2011项和S2011的最小值为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如果z∈C，且|z|=1，则|z-1-2i|的最大值为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设函数y=f（x）对任意的x∈R满足f（4+x）=f（-x），当x∈（-∞，2]时，有f（x）=2-x-5．若函数f（x）在区间（k，k+1）（k∈Z）上有零点，则k的值为（　　）
    A、-3或7B、-4或7
    C、-4或6D、-3或6

    查看答案和解析>>

    科目：高中数学 来源： 题型：

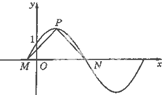    如图，函数y=2sin（πx+φ），x∈R（其中0≤φ≤
    π
    2
    ）的图象与y轴交于点（0，1）．设P是图象上的最高点，M、N是图象与x轴的交点，则PM与PN的夹角的余弦值为（　　）
    A、
    3
    5
    B、-
    3
    5
    C、
    15
    17
    D、-
    15
    17

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    某奶茶店为了了解奶茶销售量与气温之间的关系，随机统计并制作了6天卖出的奶茶的杯数与气温的对照表：
    气温x（℃） 26 19 14 10 4 -1
    杯数y 201 242 339 383 505 640
    经检验，这组样本数据具有线性相关关系，那么，对于气温x（℃）与奶茶销售量y这两个变量，下列判断正确的是（　　）
    A、成正相关，其回归直线经过点（13，385）
    B、成负相关，其回归直线经过点（13，386）
    C、成正相关，其回归直线经过点（12，386）
    D、成负相关，其回归直线经过点（12，385）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    一只艘船以均匀的速度由A点向正北方向航行，如图，开始航行时，从A点观测灯塔C的方位角（从正北方向顺时针转到目标方向的水平角）为45°，行驶60海里后，船在B点观测灯塔C的方位角为75°，则A到C的距离是（　　）海里．
    A、30（
    		6
    +
    		2
    ）
    B、30（
    		6
    -
    		2
    ）
    C、30（
    		6
    -
    		3
    ）
    D、30（
    		6
    +
    		3
    ）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知双曲线
    x2
    a2
    -
    y2
    b2
    =1(b＞a＞0)    的两条渐近线为l1，l2，过右焦点F作垂直l1的直线交l1，l2于A，B两点．若|OA|，|AB|，|OB|成等差数列，则双曲线的离心率为（　　）
    A、
    		5
    2
    B、
    		5
    C、
    		3
    D、
    		3
    +1

    查看答案和解析>>

    同步练习册答案