
已知椭圆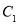 的中心在原点、焦点在
的中心在原点、焦点在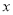 轴上,抛物线
轴上,抛物线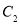 的顶点在原点、焦点在
的顶点在原点、焦点在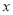 轴上.小明从曲线
轴上.小明从曲线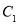 、
、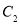 上各取若干个点(每条曲线上至少取两个点),并记录其坐标(
上各取若干个点(每条曲线上至少取两个点),并记录其坐标(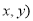 .由于记录失误,使得其中恰有一个点既不在椭圆
.由于记录失误,使得其中恰有一个点既不在椭圆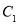 上,也不在抛物线
上,也不在抛物线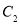 上,小明的记录如下:
上,小明的记录如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
据此,可推断椭圆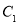 的方程为
的方程为
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源:2015届福建省高二下学期期中考试理科数学试卷(解析版) 题型:解答题
已知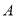 、
、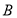 两盒中都有红球、白球,且球的形状、大小都相同,盒子
两盒中都有红球、白球,且球的形状、大小都相同,盒子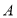 中有
中有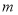 个红球与
个红球与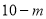 个白球,盒子
个白球,盒子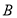 中有
中有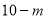 个红球与
个红球与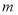 个白球(
个白球(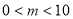 ).
).
(1)分别从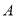 、
、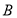 中各取一个球,
中各取一个球,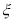 表示红球的个数;
表示红球的个数;
①请写出随机变量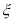 的分布列,并证明
的分布列,并证明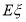 等于定值;
等于定值;
②当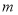 为何值时,
为何值时,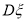 取到最小值,并求出最小值.
取到最小值,并求出最小值.
(2)在盒子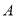 中不放回地摸取3个球,事件
中不放回地摸取3个球,事件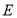 :在第一次取到红球后,以后两次都取到白球,事件
:在第一次取到红球后,以后两次都取到白球,事件 :在第一次取到白球后,以后两次都取到红球,若概率
:在第一次取到白球后,以后两次都取到红球,若概率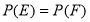 ,求
,求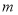 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2015届福建漳州实验中学高二(上)期末考试理科数学试卷(解析版) 题型:选择题
用系统抽样法从160名学生中抽取容量为20的样本,将160名学生从1~160编号,按编号顺序平均分成20组(1~8号,9~16号,。。。,153~160号).若第15组应抽出的号码为116,则第一组中用抽签方法确定的号码是( )
A.4 B.5 C.6 D.7
查看答案和解析>>
科目:高中数学 来源:2015届福建漳州实验中学高二(上)期末考试文科数学试卷(解析版) 题型:解答题
如图,抛物线关于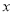 轴对称,它的顶点在坐标原点,点
轴对称,它的顶点在坐标原点,点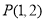 、
、 、
、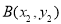 均在抛物线上.
均在抛物线上.
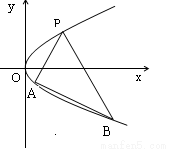
(1)写出该抛物线的方程及其准线方程;
(2)当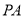 与
与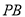 的斜率存在且倾斜角互补时,求
的斜率存在且倾斜角互补时,求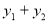 的值及直线
的值及直线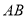 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源:2015届福建漳州实验中学高二(上)期末考试文科数学试卷(解析版) 题型:选择题
从装有除颜色外完全相同的2个红球和2个白球的口袋内任取2个球,那么互斥而不对立的两个事件是( )
A.至少有1个白球,都是白球 B.至少有1个白球,至少有1个红球
C.恰有1个白球,恰有2个白球 D.至少有1个白球,都是红球
查看答案和解析>>
科目:高中数学 来源:2015届甘肃省高二下学期6月月考数学试卷(解析版) 题型:选择题
如图是2013年中央电视台举办的挑战主持人大赛上,七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为 ( )

A.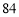 ,
,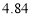 B.
B.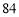 ,
,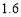 C.
C.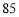 ,
,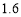 D.
D.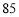 ,
,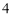
查看答案和解析>>
科目:高中数学 来源:2015届甘肃省高二下学期期末考试文科数学试卷(解析版) 题型:选择题
经过点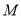 (1,5)且倾斜角为
(1,5)且倾斜角为 的直线,以定点M到动点P的位移
的直线,以定点M到动点P的位移 为参数的参数方程是( ).
为参数的参数方程是( ).
A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com