
已知正项数列{ }的前
}的前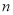 项和为
项和为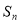 ,且
,且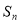 ,
, ,
,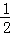 成等差数列.
成等差数列.
(1)证明数列{ }是等比数列;
}是等比数列;
(2)若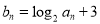 ,求数列
,求数列 的前
的前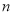 项和
项和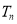 .
.
(1)证明见解析;(2)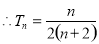
【解析】
试题分析:(1)证明一个数列是否为等差数列的基本方法有两种:一是定义法:证明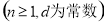 ;二是等差中项法,证明
;二是等差中项法,证明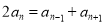 ,若证明一个数列不是等差数列,则只需举出反例即可;(2)等比数列基本量的求解是等比数列的一类基本问题,解决这类问题的关键在于熟练掌握等比数列的有关公式并能灵活运用,(3)观测数列的特点形式,看使用什么方法求和.使用裂项法求和时,要注意正负项相消时消去了哪些项,保留了哪些项,切不可漏写未被消去的项,未被消去的项有前后对称的特点,实质上造成正负相消是此法的根源和目的.
,若证明一个数列不是等差数列,则只需举出反例即可;(2)等比数列基本量的求解是等比数列的一类基本问题,解决这类问题的关键在于熟练掌握等比数列的有关公式并能灵活运用,(3)观测数列的特点形式,看使用什么方法求和.使用裂项法求和时,要注意正负项相消时消去了哪些项,保留了哪些项,切不可漏写未被消去的项,未被消去的项有前后对称的特点,实质上造成正负相消是此法的根源和目的.
试题解析:【解析】
(1)证明:由题意知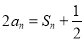
当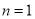 时,
时,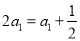 ,
,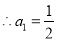
当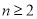 时,
时,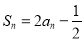 ,
,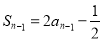
两式相减得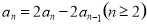 ,即
,即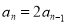
由于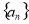 为正项数列,
为正项数列,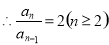
即数列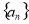 从第二项起,每一项与它前一项之比都是同一个常数2
从第二项起,每一项与它前一项之比都是同一个常数2
 数列
数列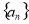 是以
是以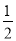 为首项,以2为公比的等比数列
为首项,以2为公比的等比数列
由(1)知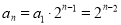 ,
,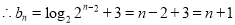
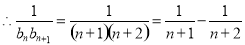
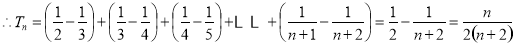 .
.
考点:1、证明数列为等比数列;2、裂项求和.


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源:2015届山东省菏泽市高三上学期期中联考文科数学试卷(解析版) 题型:选择题
函数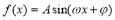 (其中
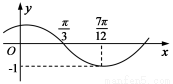
(其中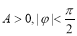 )的图象如图所示,为了得到
)的图象如图所示,为了得到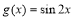 的图象,则只要将f (x)的图象( )
的图象,则只要将f (x)的图象( )
A.向右平移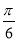 个单位长度
个单位长度
B.向右平移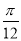 个单位长度
个单位长度
C.向左平移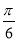 个单位长度
个单位长度
D.向左平移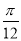 个单位长度
个单位长度
查看答案和解析>>
科目:高中数学 来源:2015届山东省高三第一次检测理科数学试卷(解析版) 题型:选择题
为了得到 的图像,只需要将
的图像,只需要将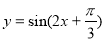 ( )
( )
A.向左平移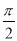 个单位 B.向右平移
个单位 B.向右平移 个单位
个单位
C.向左平移 个单位 D.向右平移
个单位 D.向右平移 个单位
个单位
查看答案和解析>>
科目:高中数学 来源:2015届山东省高三第一次检测文科数学试卷(解析版) 题型:选择题
已知函数f(x)=sin x- x(x∈[0,π]),那么下列结论正确的是 ( ).
x(x∈[0,π]),那么下列结论正确的是 ( ).
A.f(x)在 上是增函数
上是增函数
B.f(x)在 上是减函数
上是减函数
C.?x∈ ,
,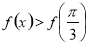
D.?x∈ ,
, 。
。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com