
以直角坐标系的原点O为极点,x轴的正半轴为极轴,且两个坐标系取相等的长度单位,已知直线  的参数方程为
的参数方程为 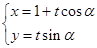 (t为参数,
(t为参数, 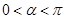 ),曲线C的极坐标方程为
),曲线C的极坐标方程为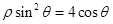 .
.
(Ⅰ)求曲线C的直角坐标方程。
(Ⅱ)设直线  与曲线C相交于A,B两点,当a变化时,求
与曲线C相交于A,B两点,当a变化时,求 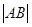 的最小值
的最小值
(Ⅰ) (Ⅱ)4
(Ⅱ)4
解析试题分析:(Ⅰ)将 两边乘以
两边乘以 得,
得, ,将
,将 代入上式得曲线C的直角坐标方程;(Ⅱ)将将直线
代入上式得曲线C的直角坐标方程;(Ⅱ)将将直线 的参数方程代入曲线C的普通方程中,整理关于t的二次方程,设M,N两点对应的参数分别为
的参数方程代入曲线C的普通方程中,整理关于t的二次方程,设M,N两点对应的参数分别为 ,利用一元二次方程根与系数将
,利用一元二次方程根与系数将 ,
, 用
用 表示出来,利用直线参数方程中参数t的几何意义得,|AB|=
表示出来,利用直线参数方程中参数t的几何意义得,|AB|= ,再转化为关于
,再转化为关于 与
与 的函数,利用前面
的函数,利用前面 ,
, 关于
关于 的表示式,将上述函数化为关于
的表示式,将上述函数化为关于 的函数,利用求最值的方法即可求出|AB|的最小值.
的函数,利用求最值的方法即可求出|AB|的最小值.
试题解析:(Ⅰ)由 ,得
,得
所以曲线C的直角坐标方程为 (4分)
(4分)
(Ⅱ)将直线l的参数方程代入 ,得
,得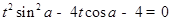
设A、B两点对应的参数分别为t1、t2,则
t1+t2=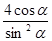 ,t1t2=
,t1t2= ,
,
∴|AB|=|t1-t2|= =
= ,
,
当 时,|AB|的最小值为4 (10分)
时,|AB|的最小值为4 (10分)
考点: 极坐标方程与直角坐标互化,直线与抛物线的位置关系,直线的参数方程中参数t的几何意义,设而不求思想


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案科目:高中数学 来源: 题型:解答题
已知曲线C1: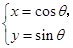 (
(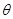 为参数),曲线C2:
为参数),曲线C2: (t为参数).
(t为参数).
(1)指出C1,C2各是什么曲线,并说明C1与C2公共点的个数;
(2)若把C1,C2上各点的纵坐标都压缩为原来的一半,分别得到曲线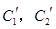 .写出
.写出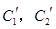 的参数方程.
的参数方程.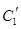 与
与 公共点的个数和C
公共点的个数和C 公共点的个数是否相同?说明你的理由.
公共点的个数是否相同?说明你的理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在直角坐标系 中,曲线
中,曲线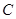 的参数方程为
的参数方程为 (
( 为参数),若以直角坐标系
为参数),若以直角坐标系 的
的 点为极点,
点为极点,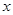 轴正方向为极轴,且长度单位相同,建立极坐标系,得直线
轴正方向为极轴,且长度单位相同,建立极坐标系,得直线 的极坐标方程为
的极坐标方程为 .求直线
.求直线 与曲线
与曲线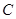 交点的极坐标.
交点的极坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知在直角坐标系xOy中,圆锥曲线C的参数方程为 (θ为参数),直线l经过定点P(2,3),倾斜角为
(θ为参数),直线l经过定点P(2,3),倾斜角为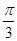 .
.
(Ⅰ)写出直线l的参数方程和圆的标准方程;
(Ⅱ)设直线l与圆相交于A,B两点,求|PA|·|PB|的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com