
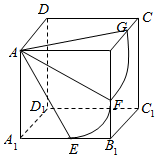
 如图,正方体ABCD-A1B1C1D1的棱长为$\sqrt{3}$,以顶点A为球心,2为半径作一个球,则图中球面与正方体的表面相交所得到的两段弧长之和($\widehat{GF}$+$\widehat{EF}$)等于$\frac{5π}{6}$.
如图,正方体ABCD-A1B1C1D1的棱长为$\sqrt{3}$,以顶点A为球心,2为半径作一个球,则图中球面与正方体的表面相交所得到的两段弧长之和($\widehat{GF}$+$\widehat{EF}$)等于$\frac{5π}{6}$. 分析 球面与正方体的六个面都相交,所得的交线分为两类:一类在顶点A所在的三个面上,即面AA1B1B、面ABCD和面AA1D1D上;另一类在不过顶点A的三个面上,即面BB1C1C、面CC1D1D和面A1B1C1D1上.由空间几何知识能求出这两段弧的长度之和.
解答  解:如图,球面与正方体的六个面都相交,
解:如图,球面与正方体的六个面都相交,
所得的交线分为两类:一类在顶点A所在的三个面上,即面AA1B1B、面ABCD和面AA1D1D上;
另一类在不过顶点A的三个面上,即面BB1C1C、面CC1D1D和面A1B1C1D1上.
在面AA1B1B上,交线为弧EF且在过球心A的大圆上,因为AE=2,AA1=$\sqrt{3}$,
则∠A1AE=$\frac{π}{6}$.同理∠BAF=$\frac{π}{6}$,所以∠EAF=$\frac{π}{6}$,
故弧EF的长为:2×$\frac{π}{6}$=$\frac{π}{3}$,
而这样的弧共有三条.
在面BB1C1C上,交线为弧FG且在距球心为1的平面与球面相交所得的小圆上,
此时,小圆的圆心为B,半径为1,∠FBG=$\frac{π}{2}$,
所以弧FG的长为:1×$\frac{π}{2}$=$\frac{π}{2}$.
于是,所得的曲线长为$\widehat{GF}$+$\widehat{EF}$=$\frac{π}{3}$+$\frac{π}{2}$=$\frac{5π}{6}$.
故答案为:$\frac{5π}{6}$.
点评 本题考查空间几何的性质和综合应用,解题时要认真审题,仔细解答,注意合理地进行等价转化.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{5}{6}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
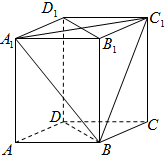 如图,长方体ABCD-A1B1C1D1中,AB=BC=2a,AA1=3a.
如图,长方体ABCD-A1B1C1D1中,AB=BC=2a,AA1=3a.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
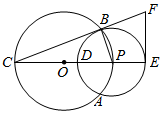 如图,⊙O与⊙P相交于A,B两点,点P在⊙O上,⊙O的弦BC切⊙P于点B,CP及其延长线交⊙P于D,E两点,过点E作EF⊥CE交CB的延长线于点F.
如图,⊙O与⊙P相交于A,B两点,点P在⊙O上,⊙O的弦BC切⊙P于点B,CP及其延长线交⊙P于D,E两点,过点E作EF⊥CE交CB的延长线于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com