
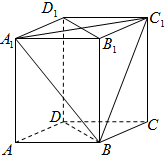
 如图,长方体ABCD-A1B1C1D1中,AB=BC=2a,AA1=3a.
如图,长方体ABCD-A1B1C1D1中,AB=BC=2a,AA1=3a.分析 (Ⅰ)证明A1C1⊥平面BB1D1D,再证明:平面A1BC1⊥平面BDD1B1;
(Ⅱ)由${V_{{B_1}-{A_1}B{C_1}}}={V_{B-{A_1}{B_1}{C_1}}}$,求点B1到平面A1BC1的距离.
解答 (Ⅰ)证明:长方体ABCD-A1B1C1D1中,BB1⊥平面A1B1C1D1,A1C1?平面A1B1C1D1,
∴BB1⊥A1C1…(2分)
又AB=BC=2a,A1B1C1D1是正方形,∴B1D1⊥A1C1…(3分)
∵B1D1∩BB1=B1,B1D1,BB1?平面BB1D1D,∴A1C1⊥平面BB1D1D…(5分)
∵A1C1?平面A1BC1,∴平面A1BC1⊥平面BDD1B1…(6分)
(Ⅱ)解:长方体ABCD-A1B1C1D1中,AB=BC=2a,AA1=3a,
则${A_1}B=B{C_1}=\sqrt{13}a,{A_1}{C_1}=2\sqrt{2}a$,…(7分)
于是△A1BC1的面积S=$\frac{1}{2}•2\sqrt{2}a•\sqrt{13{a^2}-2{a^2}}=\sqrt{22}{a^2}$…(9分)
记“点B1到平面A1BC1的距离”为h,由${V_{{B_1}-{A_1}B{C_1}}}={V_{B-{A_1}{B_1}{C_1}}}$,
得$\frac{1}{3}×\sqrt{22}{a^2}×h=\frac{1}{3}×\frac{1}{2}×2a×2a×3a$…(11分),解得$h=\frac{{3\sqrt{22}}}{11}a$…(12分)
点评 本题考查平面和平面垂直的判定和性质以及点到面的距离和三棱锥的体积计算公式.是对立体几何知识的综合考查.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
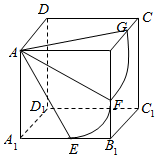 如图,正方体ABCD-A1B1C1D1的棱长为$\sqrt{3}$,以顶点A为球心,2为半径作一个球,则图中球面与正方体的表面相交所得到的两段弧长之和($\widehat{GF}$+$\widehat{EF}$)等于$\frac{5π}{6}$.
如图,正方体ABCD-A1B1C1D1的棱长为$\sqrt{3}$,以顶点A为球心,2为半径作一个球,则图中球面与正方体的表面相交所得到的两段弧长之和($\widehat{GF}$+$\widehat{EF}$)等于$\frac{5π}{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
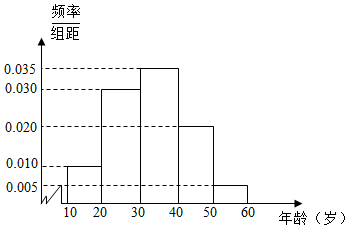 随着网络信息时代的来临,支付宝已经实现了许多功能,如购物付款、加油付款、理财产品等,使得越来越多的人在生活中使用手机支付的便捷功能,阿里巴巴公司研究人员对某地区年龄在10~60岁间的n位市民对支付宝的使用情况作出调查,并将调查的人员的年龄情况绘制成频率分布直方图如图所示.
随着网络信息时代的来临,支付宝已经实现了许多功能,如购物付款、加油付款、理财产品等,使得越来越多的人在生活中使用手机支付的便捷功能,阿里巴巴公司研究人员对某地区年龄在10~60岁间的n位市民对支付宝的使用情况作出调查,并将调查的人员的年龄情况绘制成频率分布直方图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {(${\frac{2}{3}$,$\frac{5}{3}})$)} | B. | ($\frac{2}{3}$,$\frac{5}{3}}$) | C. | {${\frac{2}{3}$,$\frac{5}{3}}$} | D. | {(${\frac{2}{3}$,$\frac{5}{3}}$),(-$\frac{2}{3}$,-$\frac{5}{3}}$)} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com