
分析 (1)设z=a+bi,则依题意得(3+4i)(a+bi)=3a-4b+(3b+4a)i为纯虚数,且|z|=1,列出方程组,求解即可得答案;
(2)利用二项式定理系数的性质,求出n,然后通过二项式定理的通项公式求出常数项即可.
解答 解:(1)设z=a+bi,则依题意得(3+4i)(a+bi)=3a-4b+(3b+4a)i为纯虚数,且|z|=1,
∴$\left\{\begin{array}{l}3a-4b=0\\{a^2}+{b^2}=1\\ 3b+4a≠0\end{array}\right.$,解之得$\left\{\begin{array}{l}a=\frac{4}{5}\\ b=\frac{3}{5}\end{array}\right.$或$\left\{\begin{array}{l}a=-\frac{4}{5}\\ b=-\frac{3}{5}\end{array}\right.$,
∴$\overline{z}=\frac{4}{5}-\frac{3}{5}i$或$\overline{z}=-\frac{4}{5}+\frac{3}{5}i$;
(2)依题意得2n=64,∴n=6.
展开式中第r+1项为${T}_{r+1}{=C}_{n}^{r}{2}^{n-r}{x}^{\frac{6-r}{2}}(-1)^{r}{x}^{-\frac{r}{2}}$=$(-1{)^{r}C}_{n}^{r}{2}^{n-r}{x}^{3-r}$,
当3-r=0时,即r=3,
∴${T}_{4}=(-1{)^{3}C}_{6}^{3}{2}^{3}=-160$.
点评 本题考查了复数代数形式的乘除运算,考查了二项式定理系数的性质,通项公式的应用,考查计算能力,是中档题.


科目:高中数学 来源: 题型:解答题
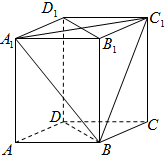 如图,长方体ABCD-A1B1C1D1中,AB=BC=2a,AA1=3a.
如图,长方体ABCD-A1B1C1D1中,AB=BC=2a,AA1=3a.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
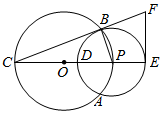 如图,⊙O与⊙P相交于A,B两点,点P在⊙O上,⊙O的弦BC切⊙P于点B,CP及其延长线交⊙P于D,E两点,过点E作EF⊥CE交CB的延长线于点F.
如图,⊙O与⊙P相交于A,B两点,点P在⊙O上,⊙O的弦BC切⊙P于点B,CP及其延长线交⊙P于D,E两点,过点E作EF⊥CE交CB的延长线于点F.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com