
分析 求导,根据导函数的正负判断原函数的单调性,通过讨论一次函数一次项系数得出单调区间.
解答 解:由已知得函数f(x)的定义域为(0,+∞),
∵f′(x)=$\frac{ax-a-1}{x}$(a≥-1),
(1)当-1≤a≤0时,f′(x)<0,函数f(x)在(0,+∞)上单调递减,
(2)当a>0时,由f′(x)=0,解得x=1$+\frac{1}{a}$.
当x∈(0,1$+\frac{1}{a}$ )时,f′(x)<0,函数f(x)在(0,1$+\frac{1}{a}$ )上单调递减.
当x∈(1$+\frac{1}{a}$,+∞)时,f′(x)>0,函数f(x)在(1$+\frac{1}{a}$,+∞)上单调递增.
综上所述:
当-1≤a≤0时,函数f(x)在(0,+∞)上单调递减.
当a>0时,函数f(x)在(0,1$+\frac{1}{a}$ )上单调递减,函数f(x)在(1$+\frac{1}{a}$,+∞)上单调递增.
点评 考查了导函数应用和对一次函数分类讨论问题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 血清酒精含量 | [0.2‰,0.4‰) | [0.4‰,0.8‰) | [0.8‰,1.2‰) | [1.2‰,1.6‰) | [1.6‰,+∞) |
| 常人精神状态 | 君子态(愉快) | 孔雀态(炫耀) | 狮子态(打架) | 猴子态(失控) | 狗熊态(昏睡) |
| 血清酒精含量 | [0.2,0.4‰‰) | [0.4‰,0.8‰) | [0.8‰,1.2‰) | [1.2‰,1.6‰) | [1.6‰,+∞) |
| 人数 | 1 | 2 | 12 | 13 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
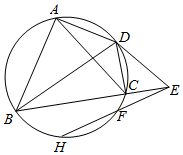 已知△ABC的外接圆为⊙O,∠B的平分线交圆O于D,过D作圆O的切线DE与BC的延长线交于E,连接AD,CD,过E再作圆的割线交圆O于F,H.
已知△ABC的外接圆为⊙O,∠B的平分线交圆O于D,过D作圆O的切线DE与BC的延长线交于E,连接AD,CD,过E再作圆的割线交圆O于F,H.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com