
| A. | $\frac{5}{2}$ | B. | $\sqrt{5}$ | C. | $\frac{9}{4}$ | D. | 3 |
分析 以B为原点建立坐标系,设A(x,y),O(cosα,sinα),根据$\overrightarrow{BO}•\overrightarrow{BA}$=1,$\overrightarrow{BO}•\overrightarrow{BC}$=$\frac{1}{2}$列方程得出x,y与α的关系,求出|$\overrightarrow{BA}+\overrightarrow{BC}+\overrightarrow{BO}$|2关于α的函数f(α),利用导数求出f(α)的最小值.
解答 解:以B为坐标原点建立平面直角坐标系,如图,设C(x,0),A(x,y).
∵|$\overrightarrow{OB}$|=1,∴O在单位圆B上.设O(cosα,sinα).
则$\overrightarrow{BO}$=(cosα,sinα),$\overrightarrow{BA}$=(x,y),$\overrightarrow{BC}=(x,0)$.
∵$\overrightarrow{BO}•\overrightarrow{BA}$=1,$\overrightarrow{BO}•\overrightarrow{BC}$=$\frac{1}{2}$,
∴$\left\{\begin{array}{l}{xcosα+ysinα=1}\\{xcosα=\frac{1}{2}}\end{array}\right.$,∴$\left\{\begin{array}{l}{xcosα=\frac{1}{2}}\\{ysinα=\frac{1}{2}}\end{array}\right.$,∴$\left\{\begin{array}{l}{x=\frac{1}{2cosα}}\\{y=\frac{1}{2sinα}}\end{array}\right.$.
∴$\overrightarrow{BA}+\overrightarrow{BC}+\overrightarrow{BO}$=(2x+cosα,y+sinα).
∴|$\overrightarrow{BA}+\overrightarrow{BC}+\overrightarrow{BO}$|2=4x2+y2+4xcosα+2ysinα+1=4x2+y2+4=$\frac{1}{co{s}^{2}α}+\frac{1}{4si{n}^{2}α}+4$.
令f(α)=$\frac{1}{co{s}^{2}α}+\frac{1}{4si{n}^{2}α}+4$.则f′(α)=$\frac{2sinα}{co{s}^{3}α}-\frac{cosα}{2si{n}^{3}α}$.
令f′(α)=0得4sin4α=cos4α.∴sin2α=$\frac{1}{3}$,cos2α=$\frac{2}{3}$.
∴fmin(α)=$\frac{3}{2}+\frac{3}{4}+4$=$\frac{25}{4}$.
∴|$\overrightarrow{BA}+\overrightarrow{BC}+\overrightarrow{BO}$|的最小值为$\sqrt{\frac{25}{4}}$=$\frac{5}{2}$.
故选:A.
点评 本题考查了平面向量的数量积运算,函数的最值,属于中档题.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2+3$\sqrt{2}$ | B. | 2+2$\sqrt{2}$ | C. | 3-2$\sqrt{2}$ | D. | 3+2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1+\sqrt{3}}{2}$ | B. | $\sqrt{\frac{8\sqrt{3}-9}{3}}$ | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1,0} | B. | {0,3} | C. | {-1,3} | D. | {-1,0,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
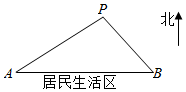 如图所示,A,B是两个垃圾中转站,B在A的正东方向16千米处,AB的南面为居民生活区,为了妥善处理生活垃圾,政府决定在AB的背面建一个垃圾发电厂P,垃圾发电厂P的选址拟满足以下两个要求(A,B,P可看成三个点):
如图所示,A,B是两个垃圾中转站,B在A的正东方向16千米处,AB的南面为居民生活区,为了妥善处理生活垃圾,政府决定在AB的背面建一个垃圾发电厂P,垃圾发电厂P的选址拟满足以下两个要求(A,B,P可看成三个点):查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com