
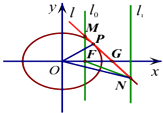
【题目】椭圆C: ![]() =1的右焦点F,过焦点F的直线l0⊥x轴,P(x0 , y0)(x0y0≠0)为C上任意一点,C在点P处的切线为l,l与l0相交于点M,与直线l1:x=3相交于N.
=1的右焦点F,过焦点F的直线l0⊥x轴,P(x0 , y0)(x0y0≠0)为C上任意一点,C在点P处的切线为l,l与l0相交于点M,与直线l1:x=3相交于N.
(I) 求证;直线 ![]() =1是椭圆C在点P处的切线;
=1是椭圆C在点P处的切线;
(Ⅱ)求证: ![]() 为定值,并求此定值;
为定值,并求此定值;
(Ⅲ)请问△ONP(O为坐标原点)的面积是否存在最小值?若存在,请求出最小及此时点P的坐标;若不存在,请说明理由.
【答案】证明:(Ⅰ)∵P(x0 , y0)在椭圆C: ![]() 上,
上,
∴ ![]() ,即
,即 ![]() ,
,
∴直线 ![]() 过点P(x0 , y0),
过点P(x0 , y0),
由 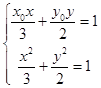 ,消去y,并利用
,消去y,并利用 ![]() ,得
,得 ![]() ,
,
即6x2﹣12x0x+6x02=0,即6(x﹣x0)2=0,∴x=x0 ,
∴直线 ![]() =1与椭圆C在点P处有且仅有一个交点,
=1与椭圆C在点P处有且仅有一个交点,
综上,直线 ![]() 是椭圆C在点P处的切线.
是椭圆C在点P处的切线.
(Ⅱ)在 ![]() 中,令x=1,得y=
中,令x=1,得y= ![]() ,∴M(1,
,∴M(1, ![]() ),
),
在 ![]() 中,令x=3,得y=
中,令x=3,得y= ![]() ,∴N(3,
,∴N(3, ![]() ),
),
又F(1,0),∴|FM|=| ![]() |=2|
|=2| ![]() |,
|,
|FN|= 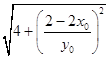 =2
=2 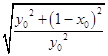 =2
=2 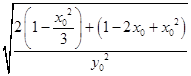 =2
=2 ![]() ,
,
∴ ![]() =
= ![]() 为定值.
为定值.
解:(Ⅲ)在直线 ![]() 中,令y=0,得x=
中,令y=0,得x= ![]() ,
,
∴切线l与x轴的交点为G( ![]() ,0),
,0),
S△ONP= 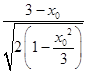 =
= 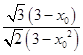 =
= 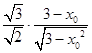
= ![]() |
| ![]() ||
|| ![]() |
|
= ![]() |
| ![]() ||
|| ![]() |
|
= 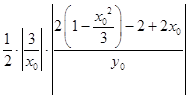
=| ![]() |=
|= ![]() ,
,
S△ONP= 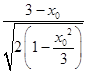 =
= 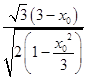 =
= 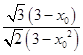 =
= 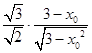 ,
,
令3﹣x0= ![]() ,由﹣
,由﹣ ![]() ,得
,得 ![]() ,且t
,且t ![]() ,
,
且 ![]() =
= 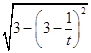 =
= ![]() =
= ![]()
![]() =
=  ,
,
∴当t= ![]() ,x0=1时,△ONP(O为坐标原点)的面积是存在最小值{S△ONP}min=
,x0=1时,△ONP(O为坐标原点)的面积是存在最小值{S△ONP}min= ![]() ,
,
此时P(1, ![]() ).
).
【解析】(Ⅰ)推导出直线 ![]() 过点P(x0 , y0),由
过点P(x0 , y0),由 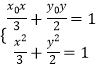 及
及 ![]() ,得
,得 ![]() ,由此能证明直线
,由此能证明直线 ![]() 是椭圆C在点P处的切线.(Ⅱ)在
是椭圆C在点P处的切线.(Ⅱ)在 ![]() 中,令x=1,M(1,
中,令x=1,M(1, ![]() ),令x=3,得N(3,
),令x=3,得N(3, ![]() ),由此求出|FM|,|FN|,由此能证明
),由此求出|FM|,|FN|,由此能证明 ![]() 为定值.(Ⅲ)求出切线l与x轴的交点为G(
为定值.(Ⅲ)求出切线l与x轴的交点为G( ![]() ,0),推导出S△ONP=
,0),推导出S△ONP= ![]() =
= ![]() ,令3﹣x0=
,令3﹣x0= ![]() ,利用配方法能求出△ONP的面积的最小值及对应的P点坐标.
,利用配方法能求出△ONP的面积的最小值及对应的P点坐标.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,已知等边△ABC中,E,F分别为AB,AC边的中点,N为BC边上一点,且CN= ![]() BC,将△AEF沿EF折到△A′EF的位置,使平面A′EF⊥平面EF﹣CB,M为EF中点.
BC,将△AEF沿EF折到△A′EF的位置,使平面A′EF⊥平面EF﹣CB,M为EF中点. 
(1)求证:平面A′MN⊥平面A′BF;
(2)求二面角E﹣A′F﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】动点![]() 在抛物线
在抛物线![]() 上,过点
上,过点![]() 作
作![]() 垂直于
垂直于![]() 轴,垂足为
轴,垂足为![]() ,设
,设![]() .
.
(Ⅰ)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)若点![]() 是
是![]() 上的动点,过点
上的动点,过点![]() 作抛物线
作抛物线![]() :
:![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,设点
,设点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求
,求![]() 的最小值。
的最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在原点,离心率等于
的中心在原点,离心率等于![]() ,它的一个短轴端点恰好是抛物线
,它的一个短轴端点恰好是抛物线![]() 的焦点.
的焦点.
(1)求椭圆![]() 的方程;
的方程;
(2)已知![]() 、
、![]() 是椭圆上的两点,
是椭圆上的两点,![]() 是椭圆上位于直线
是椭圆上位于直线![]() 两侧的动点.
两侧的动点.
①若直线![]() 的斜率为
的斜率为![]() ,求四边形
,求四边形![]() 面积的最大值;
面积的最大值;
②当![]() 运动时,满足
运动时,满足![]() ,试问直线
,试问直线![]() 的斜率是否为定值,请说明理由.
的斜率是否为定值,请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两台机床同时生产一种零件,10天中,两台机床每天出的次品数分别如下图所示。
甲 | 0 | 1 | 0 | 2 | 2 | 0 | 3 | 1 | 2 | 4 |
乙 | 2 | 3 | 1 | 1 | 0 | 2 | 1 | 1 | 0 | 1 |
从数据上看, ________________机床的性能较好(填“甲”或者“乙”).
查看答案和解析>>
科目:高中数学 来源: 题型:
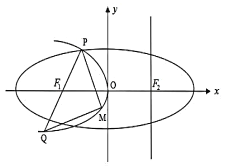
【题目】如图,设抛物线![]() 的准线
的准线![]() 与
与![]() 轴交于椭圆
轴交于椭圆![]() 的右焦点
的右焦点![]() 为
为![]() 的左焦点.椭圆的离心率为
的左焦点.椭圆的离心率为![]() ,抛物线
,抛物线![]() 与椭圆
与椭圆![]() 交于
交于![]() 轴上方一点
轴上方一点![]() ,连接
,连接![]() 并延长其交
并延长其交![]() 于点
于点![]() ,
, ![]() 为
为![]() 上一动点,且在
上一动点,且在![]() 之间移动.
之间移动.
(1)当![]() 取最小值时,求
取最小值时,求![]() 和
和![]() 的方程;
的方程;
(2)若![]() 的边长恰好是三个连续的自然数,当
的边长恰好是三个连续的自然数,当![]() 面积取最大值时,求面积最大值以及此时直线
面积取最大值时,求面积最大值以及此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 C:![]() 的焦距为2,且过点
的焦距为2,且过点![]() ,右焦点为
,右焦点为![]() .设A,B 是C上的两个动点,线段 AB 的中点M 的横坐标为
.设A,B 是C上的两个动点,线段 AB 的中点M 的横坐标为![]() ,线段AB的中垂线交椭圆C于P,Q 两点.
,线段AB的中垂线交椭圆C于P,Q 两点.
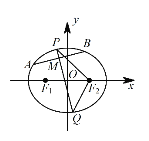
(1)求椭圆 C 的方程;
(2)设M点纵坐标为m,求直线PQ的方程,并求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
将边长为2的正方形ABCD沿对角线BD折叠,使得平面ABD⊥平面CBD,AE⊥平面ABD,且AE=![]() .
.
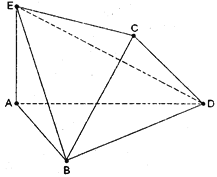
(Ⅰ)求证:DE⊥AC;
(Ⅱ)求DE与平面BEC所成角的正弦值;
(Ⅲ)直线BE上是否存在一点M,使得CM∥平面ADE,若存在,求点M的位置,不存在请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com