Question

【题目】如图，已知等边△ABC中，E，F分别为AB，AC边的中点，N为BC边上一点，且CN= BC，将△AEF沿EF折到△A′EF的位置，使平面A′EF⊥平面EF﹣CB，M为EF中点．

（1）求证：平面A′MN⊥平面A′BF；
（2）求二面角E﹣A′F﹣B的余弦值．

Answer 1

【答案】
（1）证明：如图所示，取BC的中点G，连接MG，则MG⊥EF，

∵平面A′EF⊥平面EFCB，平面A′EF∩平面EFCB=EF，

∴MG⊥平面A′EF，∴MG⊥A′M，又A′M⊥EF，

因此可以建立空间直角坐标系．不妨设BC=4．

M（0，0，0），A′（0，0， ），N（﹣1， ，0），

B（2， ，0），F（﹣1，0，0）．

=（0，0， ）， =（﹣1， ，0），

=（1，0， ）， =（3， ，0）．

设平面A′MN的法向量为 =（x，y，z），

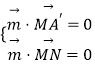则 ，即 ，

取 = ．

同理可得平面A′BF的法向量 = ．

∵ =3﹣3+0=0，∴ ，

∴平面A′MN⊥平面A′BF

（2）解：由（1）可得平面A′BF的法向量 = ．

取平面EA′F的法向量 =（0，1，0）．

则cos = = =- ，

由图可知：二面角E﹣A′F﹣B的平面角为锐角，

∴二面角E﹣A′F﹣B的平面角的余弦值为 ．

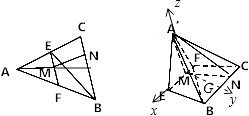
【解析】（1）如图所示，取BC的中点G，连接MG，则MG⊥EF，利用面面与线面垂直的性质与判定定理可得：MG⊥A′M，又A′M⊥EF，因此可以建立空间直角坐标系．不妨设BC=4．只要证明平面法向量的夹角为直角即可证明平面A′MN⊥平面A′BF．（2）利用两个平面的法向量的夹角即可得出．
【考点精析】本题主要考查了平面与平面垂直的判定的相关知识点，需要掌握一个平面过另一个平面的垂线，则这两个平面垂直才能正确解答此题．