
【题目】动点![]() 在抛物线
在抛物线![]() 上,过点
上,过点![]() 作
作![]() 垂直于
垂直于![]() 轴,垂足为
轴,垂足为![]() ,设
,设![]() .
.
(Ⅰ)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)若点![]() 是
是![]() 上的动点,过点
上的动点,过点![]() 作抛物线
作抛物线![]() :
:![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,设点
,设点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求
,求![]() 的最小值。
的最小值。
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设直线l:y=2x+2,若l与椭圆![]() 的交点为A,B,点P为椭圆上的动点,则使△PAB的面积为
的交点为A,B,点P为椭圆上的动点,则使△PAB的面积为![]() 的点P的个数为( )
的点P的个数为( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某海礁A处有一风暴中心,距离风暴中心A正东方向200km的B处有一艘轮船,正以北偏西a(a为锐角)角方向航行,速度为40km/h.已知距离风暴中心180km以内的水域受其影响.
(1)若轮船不被风暴影响,求角α的正切值的最大值?
(2)若轮船航行方向为北偏西45°,求轮船被风暴影响持续多少时间?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有如下3个命题;
①双曲线![]() 上任意一点
上任意一点![]() 到两条渐近线的距离乘积是定值;
到两条渐近线的距离乘积是定值;
②双曲线![]() 的离心率分别是
的离心率分别是![]() ,则
,则![]() 是定值;
是定值;
③过抛物线![]() 的顶点任作两条互相垂直的直线与抛物线的交点分别是
的顶点任作两条互相垂直的直线与抛物线的交点分别是![]() ,则直线
,则直线![]() 过定点;其中正确的命题有( )
过定点;其中正确的命题有( )
A. 3个 B. 2个 C. 1个 D. 0个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的焦距为
的焦距为![]() ,离心率为
,离心率为![]() ,椭圆的右顶点为
,椭圆的右顶点为![]() .
.

(1)求该椭圆的方程;
(2)过点![]() 作直线
作直线![]() 交椭圆于两个不同点
交椭圆于两个不同点![]() ,求证:直线
,求证:直线![]() 的斜率之和为定值.
的斜率之和为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线C:![]() (a>0,b>0)的渐近线方程为y=±
(a>0,b>0)的渐近线方程为y=±![]() x,O为坐标原点,点
x,O为坐标原点,点![]() 在双曲线上.
在双曲线上.
(I)求双曲线C的方程.
(II)若斜率为1的直线l与双曲线交于P,Q两点,且![]() =0,求直线l方程.
=0,求直线l方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆C: ![]() =1的右焦点F,过焦点F的直线l0⊥x轴,P(x0 , y0)(x0y0≠0)为C上任意一点,C在点P处的切线为l,l与l0相交于点M,与直线l1:x=3相交于N.
=1的右焦点F,过焦点F的直线l0⊥x轴,P(x0 , y0)(x0y0≠0)为C上任意一点,C在点P处的切线为l,l与l0相交于点M,与直线l1:x=3相交于N.
(I) 求证;直线 ![]() =1是椭圆C在点P处的切线;
=1是椭圆C在点P处的切线;
(Ⅱ)求证: ![]() 为定值,并求此定值;
为定值,并求此定值;
(Ⅲ)请问△ONP(O为坐标原点)的面积是否存在最小值?若存在,请求出最小及此时点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的程序框图的算法思路源于我国古代数学中的秦九韶算法,执行该程序框图,则输出的结果S表示的值为( ) 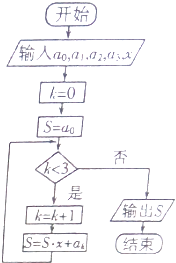
A.a0+a1+a2+a3
B.(a0+a1+a2+a3)x3
C.a0+a1x+a2x2+a3x3
D.a0x3+a1x2+a2x+a3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com