
【题目】己知函数![]() ,
, ![]() .
.
(I)求函数![]() 的单调区间;
的单调区间;
(II)设![]() ,已知函数
,已知函数![]() 在
在![]() 上是增函数.
上是增函数.
(1)研究函数![]() 上零点的个数;
上零点的个数;
(ii)求实数c的取值范围.
【答案】(Ⅰ)详见解析; (Ⅱ)(1)1个;(2) ![]() .
.
【解析】试题分析(1) 对函数求导,①当![]() 时,
时, ![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数;②当
上是增函数;②当![]() 时,
时, ![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数;(2) (1)当
上是减函数;(2) (1)当![]() 时,函数
时,函数![]()
![]() ,
, ![]() ,
, ![]() 在
在![]() 上单调递减.又
上单调递减.又![]() ,
, ![]() ,由函数的零点存在性定理及其单调性知,
,由函数的零点存在性定理及其单调性知, ![]() 在
在![]() 上零点的个数为1.(2)由(1)知,当
上零点的个数为1.(2)由(1)知,当![]() 时,
时, ![]() >0,当
>0,当![]() 时,
时, ![]() <0.∴当
<0.∴当![]() 时,
时, ![]() =
=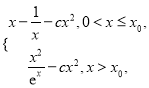 求导,得
求导,得![]() 在
在![]() ,
, ![]() 上恒成立. ①当
上恒成立. ①当![]() 时,
时, ![]() min=
min= ![]() 极小值=
极小值= ![]()
![]() ,故“
,故“![]() 在
在![]() 上恒成立”,只需
上恒成立”,只需![]()
![]() .②当
.②当![]() 时,当
时,当![]() 时,
时, ![]() 在
在![]() 上恒成立,综合①②知,
上恒成立,综合①②知, ![]() 的取值范围是
的取值范围是![]() .
.
试题解析:(Ⅰ)∵![]() ,
,
∴![]() ,
,
①当![]() 时,
时,
在![]() 时,
时, ![]() ,
,
在![]() 时,
时, ![]() ,
,
故![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数;
上是增函数;
②当![]() 时,
时,
在![]() 时,
时, ![]() ,
,
在![]() 时,
时, ![]() ,
,
故![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数;
上是减函数;
(Ⅱ)(1)当![]() 时,函数
时,函数![]()
![]() ,
,
求导,得![]() ,
,
当![]() 时,
时, ![]() 恒成立,
恒成立,
当![]() 时,
时, 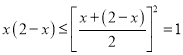 ,
,
∴![]()
![]() ,
,
∴![]() 在
在![]() 上恒成立,故
上恒成立,故![]() 在
在![]() 上单调递减.
上单调递减.
又![]() ,
, ![]() ,
,
曲线![]() 在[1,2]上连续不间断,
在[1,2]上连续不间断,
∴由函数的零点存在性定理及其单调性知,唯一的![]() ∈(1,2),使
∈(1,2),使![]() ,
,
所以,函数![]() 在
在![]() 上零点的个数为1.
上零点的个数为1.
(2)由(1)知,当![]() 时,
时, ![]() >0,当
>0,当![]() 时,
时, ![]() <0.
<0.
∴当![]() 时,
时, ![]() =
=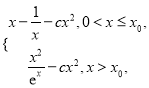
求导,得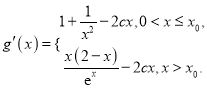
由函数![]() 在
在![]() 上是增函数,且曲线
上是增函数,且曲线![]() 在
在![]() 上连续不断知:
上连续不断知:
![]() 在
在![]() ,
, ![]() 上恒成立.
上恒成立.
①当![]() 时,
时, ![]()
![]() 上恒成立,
上恒成立,
即![]() 在
在![]() 上恒成立,
上恒成立,
记![]() ,
, ![]() ,则
,则![]() ,
, ![]() ,
,
当 ![]() 变化时,
变化时, ![]() ,
, ![]() 变化情况列表如下:
变化情况列表如下:
|
| 3 |
|
|
| 0 |
|
|
| 极小值 |
|
∴![]() min=
min= ![]() 极小值=
极小值= ![]()
![]() ,
,
故“![]() 在
在![]() 上恒成立”,只需
上恒成立”,只需![]()
![]() ,即
,即![]() .
.
②当![]() 时,
时, ![]()
![]() ,
,
当![]() 时,
时, ![]() 在
在![]() 上恒成立,
上恒成立,
综合①②知,当![]() 时,函数
时,函数![]() 在
在![]() 上是增函数.
上是增函数.
故实数![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】如图是某社区工会对当地企业工人月收入情况进行一次抽样调查后画出的频率分布直方图,其中第二组月收入在[1.5,2)千元的频数为300,则此次抽样的样本容量为( ) 
A.1000
B.2000
C.3000
D.4000
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCED中,PD⊥面ABCD,四边形ABCD为平行四边形,∠DAB=60°,AB=PA=2AD=4, 
(1)若E为PC中点,求证:PA∥平面BDE
(2)求三棱锥D﹣BCP的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 过点
过点![]() ,
, ![]() 为椭圆的半焦距,且
为椭圆的半焦距,且![]() ,过点
,过点![]() 作两条互相垂直的直线
作两条互相垂直的直线![]() ,
, ![]() 与椭圆
与椭圆![]() 分别交于另两点
分别交于另两点![]() ,
, ![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 的斜率为
的斜率为![]() ,求
,求![]() 的面积;
的面积;
(3)若线段![]() 的中点在
的中点在![]() 轴上,求直线
轴上,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数,函数
上是增函数,函数![]() 在
在![]() 上有三个零点.
上有三个零点.
(1)求![]() 的值;
的值;
(2)若1是其中一个零点,求![]() 的取值范围;
的取值范围;
(3)若![]() ,试问过点(2,5)可作多少条直线与曲线y=g(x)相切?请说明理由.
,试问过点(2,5)可作多少条直线与曲线y=g(x)相切?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
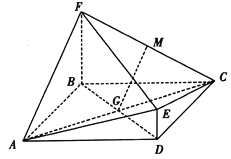
【题目】如图,菱![]() 与四边形BDEF相交于BD,
与四边形BDEF相交于BD, ![]() 平面ABCD,DE//BF,BF=2DE,AF⊥FC,M为CF的中点,
平面ABCD,DE//BF,BF=2DE,AF⊥FC,M为CF的中点, ![]() .
.
(I)求证:GM//平面CDE;
(II)求证:平面ACE⊥平面ACF.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知函数![]() (其中e为自然对数的底数),
(其中e为自然对数的底数), ![]() .
.
(I)求函数![]() 的单调区间;
的单调区间;
(II)设![]() ,.已知直线
,.已知直线![]() 是曲线
是曲线![]() 的切线,且函数
的切线,且函数![]() 上是增函数.
上是增函数.
(i)求实数![]() 的值;
的值;
(ii)求实数c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设p:实数x满足x2﹣4ax+3a2<0,其中a>0,命题q:实数x满足 ![]() .
.
(1)若a=1,且p∨q为真,求实数x的取值范围;
(2)若p是q的必要不充分要条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}满足:a3=3,a5+a7=12,{an}的前n项和为Sn .
(1)求an及Sn;
(2)令bn= ![]() (n∈N*),求数列{bn}的前n项和Tn .
(n∈N*),求数列{bn}的前n项和Tn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com