
| 2 |
| π |
| 8 |
| π |
| 8 |
| 2 |
| π |
| 8 |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 2 |
| 2 |
| 2 |
| π |
| 8 |
| π |
| 8 |
| 2 |
| π |
| 8 |
| 2 |
| π |
| 4 |
| 2 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 2π | ||
|
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 2 |
| 2 |
| 2 |
| 6 |
| 3 |
| 2 |
| ||||
|
|
2×4+
| ||||
|
| ||
| 3 |
| 1-cos2∠POQ |
| ||
| 3 |
| |PQ| |
| sin∠POQ |
| |PQ| |
| 2sin∠POQ |
2
| ||||
2×
|
3
| ||
| 2 |
| 9 |
| 2 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
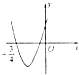 如图是函数f(x)=x2-ax+b的大致图象,则函数g(x)=log2x+f′(x)的零点所在的区间是( )
如图是函数f(x)=x2-ax+b的大致图象,则函数g(x)=log2x+f′(x)的零点所在的区间是( )A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| OA |
| a |
| b |
| OB |
| a |
| b |
| OC |
| a |
| b |
| a |
| b |
| a |
| b |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 树干周长(单位:cm) | [30,40) | [40,50) | [50,60) | [60,70) |
| 杉树 | 6 | 19 | 21 | x |
| 槐树 | 4 | 20 | y | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| PM2.5日均值(微克/立方米) | [25,35] | [35,45] | (45,55] | (55,65] | (65,75] | (75,85] |
| 频数 | 3 | 1 | 1 | 1 | 1 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| 3 |
| a |
| b |
查看答案和解析>>
科目:高中数学 来源: 题型:
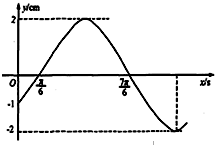 如图是某简谐运动的一段图象,其函数模型是f(x)=Asin(ωx+φ)(x≥0),其中A>0,ω>0,-
如图是某简谐运动的一段图象,其函数模型是f(x)=Asin(ωx+φ)(x≥0),其中A>0,ω>0,-| π |
| 2 |
| π |
| 2 |
| π |
| 6 |
| ∫ | π α |
查看答案和解析>>
科目:高中数学 来源: 题型:
| AB |
| AC |
| A |
| 2 |
| A |
| 2 |
| ||
| 2 |
| π |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com