
分析 画出立体图形,根据中点找平行线,把所求的异面直线角转化为一个三角形的内角来计算.
解答  解:如图,连接CF,取BF的中点M,连接CM,EM,
解:如图,连接CF,取BF的中点M,连接CM,EM,
则ME∥AF,故∠CEM即为所求的异面直线角.
设这个正四面体的棱长为2,
在△ABD中,AF=$\sqrt{3}$=CE=CF,EM=$\frac{\sqrt{3}}{2}$,CM=$\frac{\sqrt{13}}{2}$.
∴cos∠CEM=$\frac{\frac{3}{4}+3-\frac{13}{4}}{2×\frac{\sqrt{3}}{2}×\sqrt{3}}$=$\frac{1}{6}$.
故答案为$\frac{1}{6}$.
点评 本题考查空间点、线、面的位置关系及学生的空间想象能力、求异面直线角的能力.在立体几何中找平行线是解决问题的一个重要技巧,这个技巧就是通过三角形的中位线找平行线,如果试题的已知中涉及到多个中点,则找中点是出现平行线的关键技巧.


科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | -1 | C. | -2 | D. | -5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-e) | B. | (-∞,$\frac{1}{e}$) | C. | (0,$\frac{1}{e}$) | D. | (e,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
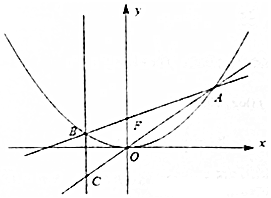 已知抛物线x2=2py(p>0),F为其焦点,过点F的直线l交抛物线于A、B两点,过点B作x轴的垂线,交直线OA于点C,如图所示.
已知抛物线x2=2py(p>0),F为其焦点,过点F的直线l交抛物线于A、B两点,过点B作x轴的垂线,交直线OA于点C,如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | [11,13) | [13,15) | [15,17) | [17,19) | [19,21) | [21,23) |
| 频数 | 2 | 12 | 34 | 38 | 10 | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com